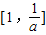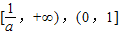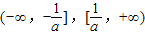题目内容
设函数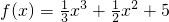
，则函数g（x）=f（logax）（0＜a＜1）的单调递增区间是
- A.
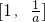
- B.
- C.
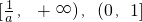
- D.
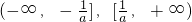
A
分析：确定内、外函数的单调性，利用函数g（x）=f（logax）（0＜a＜1）的单调递增区间，可得不等式，从而可得结论．
解答：∵函数，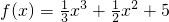
∴f′（x）=x2+x
由f′（x）≥0，可得x≤-1或x≥0；由f′（x）≤0，可得-1≤x≤0
∵y=logax（0＜a＜1）在（0，+∞）上是减函数
∴要求函数g（x）=f（logax）（0＜a＜1）的单调递增区间，则-1≤logax≤0
∴1≤x≤
故选A．
点评：本题考查复合函数的单调性，考查学生的计算能力，确定内、外函数的单调性是关键．
分析：确定内、外函数的单调性，利用函数g（x）=f（logax）（0＜a＜1）的单调递增区间，可得不等式，从而可得结论．
解答：∵函数
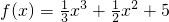，∴f′（x）=x2+x
由f′（x）≥0，可得x≤-1或x≥0；由f′（x）≤0，可得-1≤x≤0
∵y=logax（0＜a＜1）在（0，+∞）上是减函数
∴要求函数g（x）=f（logax）（0＜a＜1）的单调递增区间，则-1≤logax≤0
∴1≤x≤
故选A．
点评：本题考查复合函数的单调性，考查学生的计算能力，确定内、外函数的单调性是关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
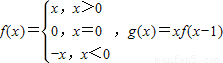，则函数g（x）的递减区间是（ ）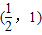
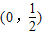
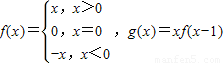，则函数g（x）的递减区间是（ ）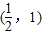
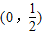
，则函数g（x）=f（x）-x的零点的个数为（ ）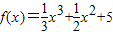
，则函数g（x）=f（logax）（0＜a＜1）的单调递增区间是（ ）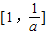
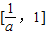
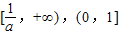
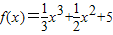，则函数g（x）=f（logax）（0＜a＜1）的单调递增区间是（ ）
