题目内容
使方程2-sin2x=m(2+sin2x)有解,则m的取值范围是 .
【答案】分析:将方程2-sin2x=m(2+sin2x)进行恒等变换可得,sin2x=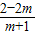 有解,根据正弦型函数的值域为[-1,1],可得一个关于m的不等式,解不等式即可得到m的取值范围.
有解,根据正弦型函数的值域为[-1,1],可得一个关于m的不等式,解不等式即可得到m的取值范围.
解答:解:若方程2-sin2x=m(2+sin2x)有解,
即方程(m+1)sin2x=2-2m有解,
即sin2x=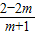 有解,
有解,
即-1≤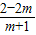 ≤1
≤1
解得m∈[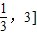
故答案为:[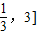
点评:本题考查的知识点是根的存在性及根的个数判断,三角函数的值域,其中根据正弦型函数的值域为[-1,1],构造关于m的不等式,是解答本题的关键.
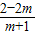 有解,根据正弦型函数的值域为[-1,1],可得一个关于m的不等式,解不等式即可得到m的取值范围.
有解,根据正弦型函数的值域为[-1,1],可得一个关于m的不等式,解不等式即可得到m的取值范围.解答:解:若方程2-sin2x=m(2+sin2x)有解,
即方程(m+1)sin2x=2-2m有解,
即sin2x=
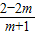 有解,
有解,即-1≤
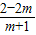 ≤1
≤1解得m∈[
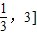
故答案为:[
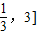
点评:本题考查的知识点是根的存在性及根的个数判断,三角函数的值域,其中根据正弦型函数的值域为[-1,1],构造关于m的不等式,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目