题目内容
已知函数f(x)=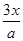 -2
-2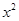 +lnx.
+lnx.
(Ⅰ)若a=1,求函数f(x)的极值;
(Ⅱ)若函数f(x)在区间[1,2]上为单调递增函数,求实数a的取值范围.
【答案】
(Ⅰ)见解析
(Ⅱ)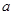 的取值范围是
的取值范围是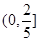 .
.
【解析】(1)当a=1时,解析式确定,可利用导数等于零,求出极值。但要注意定义域。
(II)本小题转化为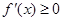 在[1,2]上恒成立,即
在[1,2]上恒成立,即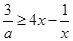 在
在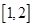 恒成立,再转化为函数最值问题求解。
恒成立,再转化为函数最值问题求解。
(Ⅰ)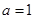 时,
时,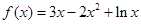 ,定义域为
,定义域为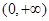 . …………1分
. …………1分
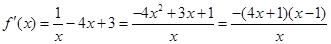
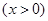 ,………3分
,………3分
当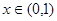 ,
,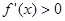 ,函数
,函数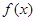 单调递增;
单调递增;
当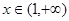 ,
,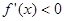 ,函数
,函数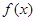 单调递减,…………………5分
单调递减,…………………5分
∴ 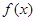 有极大值
有极大值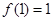 ,无极小值.………………………………6分
,无极小值.………………………………6分
(Ⅱ)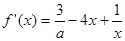 ,……7分
,……7分
∵ 函数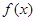 在区间
在区间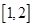 上为单调递增函数,∴
上为单调递增函数,∴
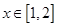 时,
时,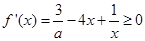 恒成立.即
恒成立.即
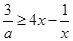 在
在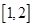 恒成立,…………9分
恒成立,…………9分
令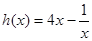 ,因函数
,因函数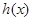 在
在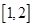 上单调递增,所以
上单调递增,所以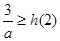 ,即
,即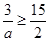 ,…11分
,…11分
解得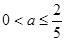 ,即
,即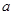 的取值范围是
的取值范围是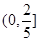 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
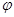 )(ω>0,0<
)(ω>0,0<
 =
= ,且a∈(0,
,且a∈(0, ),求f(a)的值.
),求f(a)的值. -a
-a +x(a>0).
+x(a>0). =
= ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程; 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: .
.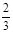 与x=1时都取得极值.
与x=1时都取得极值. ,若f(x)存在零点,则实数a的取值范围
,若f(x)存在零点,则实数a的取值范围