题目内容
已知△ABC三边所在的直线方程为AB:4x-3y+10=0,BC:y-2=0,AC:3x-4y-5=0.
(1)求过顶点A与BC边平行的直线方程;
(2)求∠BAC的内角分线所在的直线方程.
(1)求过顶点A与BC边平行的直线方程;
(2)求∠BAC的内角分线所在的直线方程.
三个方程两两联立,得
A(-
,-
),B(-1,2),C(
,2)
(1)故过顶点A与BC边平行的直线方程为:y=-
….(5分)
(2)因为∠A的角平分线上任一点到AB和AC两边的距离相同,
所以设这点为(x,y)
由点到直线距离公式可得:
点到AB=
=点到AC=
化简后有两条,舍去一条(另一条不在三角形内,是外角平分线)
得:7x-7y+5=0(10分)
A(-
| 55 |
| 7 |
| 50 |
| 7 |
| 13 |
| 3 |
(1)故过顶点A与BC边平行的直线方程为:y=-
| 50 |
| 7 |
(2)因为∠A的角平分线上任一点到AB和AC两边的距离相同,
所以设这点为(x,y)
由点到直线距离公式可得:
点到AB=
| |4x-3y+10| | ||
|
| |3x-4y-5| | ||
|
化简后有两条,舍去一条(另一条不在三角形内,是外角平分线)
得:7x-7y+5=0(10分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
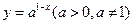 的图像恒过定点
的图像恒过定点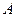 ,若点
,若点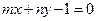
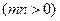 上,则
上,则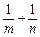 的最小值为 .
的最小值为 .