题目内容
已知x>0,y>0,x+3y=1,则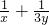 的最小值是
的最小值是
- A.

- B.2
- C.4
- D.

C
分析:先对 +
+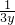 的乘以1结果保持不变,将2x+y=1看为一个整体代入得(
的乘以1结果保持不变,将2x+y=1看为一个整体代入得(  +
+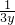 )×1=(
)×1=(  +
+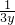 )×(3x+y),再运用基本不等式可求得最小值.
)×(3x+y),再运用基本不等式可求得最小值.
解答:∵x+3y=1,
∴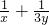 =(
=(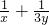 )(x+3y)=2+
)(x+3y)=2+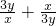
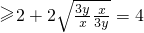
当且仅当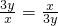 即
即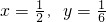 时等号成立,
时等号成立,
∴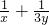 的最小值是4
的最小值是4
故选:C
点评:本题考查基本不等式常见的变形形式与运用,如本题中,1的代换.在运用基本不等式时,要注意“一正、二定、三相等”的要求.
分析:先对
 +
+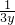 的乘以1结果保持不变,将2x+y=1看为一个整体代入得(
的乘以1结果保持不变,将2x+y=1看为一个整体代入得(  +
+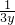 )×1=(
)×1=(  +
+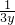 )×(3x+y),再运用基本不等式可求得最小值.
)×(3x+y),再运用基本不等式可求得最小值.解答:∵x+3y=1,
∴
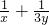 =(
=(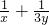 )(x+3y)=2+
)(x+3y)=2+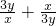
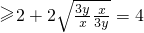
当且仅当
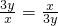 即
即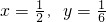 时等号成立,
时等号成立,∴
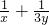 的最小值是4
的最小值是4故选:C
点评:本题考查基本不等式常见的变形形式与运用,如本题中,1的代换.在运用基本不等式时,要注意“一正、二定、三相等”的要求.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
(2007
宁夏,7)已知x>0,y>0,x,a,b,y成等差数列,x,c,d,y成等比数列,则 的最小值是
的最小值是
[
]|
A .0 |
B .1 |
C .2 |
D .4 |
 的最小值是( ) A.0 B.1 C.2 D.4
的最小值是( ) A.0 B.1 C.2 D.4