题目内容
8.掷2个骰子,至少有一个1点的概率为$\frac{11}{36}$.(用数字作答)分析 根据题意,首先利用列表法,列举出所有的情况,可得全部的情况数目以及有一个骰子点数为1的情况数目,由古典概型公式计算可得答案.
解答 解:同时掷两个质地均匀的骰子的情况有:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
则至少有一个1点的概率P(A)=$\frac{11}{36}$;
故答案为:$\frac{11}{36}$.
点评 本题考查古典概型的计算,本题中找到两个骰子点数相同的情况数和至少有一个骰子点数为3还有两个骰子的点数的和为8的情况数是关键.

练习册系列答案
相关题目
16.函数y=sin($\frac{π}{3}-\frac{x}{2}$)的最小正周期是( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
7.对某电子元件进行寿命追踪调查,情况如下.
(1)画出频率分布直方图;
(2)估计电子元件寿命在400h以上的在总体中占的比例;
(3)估计电子元件寿命的众数,中位数及平均数.
| 寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个 数 | 20 | 30 | 80 | 40 | 30 |
(2)估计电子元件寿命在400h以上的在总体中占的比例;
(3)估计电子元件寿命的众数,中位数及平均数.
5.函数$y=\frac{1}{\sqrt{{-x}^{2}+2x+3}}$的单调减区间是( )
| A. | (1,3) | B. | (-∞,1) | C. | (-1,1) | D. | [-1,1] |
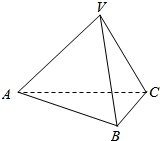 正三棱锥V-ABC的底面边长是a,侧面与底面成60°的二面角.求
正三棱锥V-ABC的底面边长是a,侧面与底面成60°的二面角.求