题目内容
函数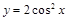 的一个单调递增区间是( )
的一个单调递增区间是( )
A.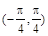 | B.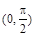 | C.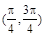 | D.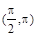 |
D
解析试题分析: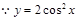 ,
, ,令
,令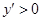 ,则
,则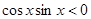 ,故选D。
,故选D。
考点:利用导函数判断函数的单调性

练习册系列答案
相关题目
函数f(x)=ax3-x在R上为减函数,则( )
| A.a≤0 | B.a<1 | C.a<0 | D.a≤1 |

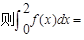 ( )
( )
A.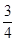 | B.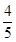 | C.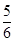 | D.不存在 |
曲线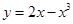 在横坐标为
在横坐标为 l的点处的切线为
l的点处的切线为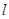 ,则直线
,则直线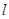 的方程为( )
的方程为( )
A.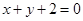 | B.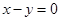 | C.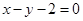 | D.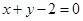 |
若 则
则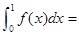 ( )
( )
A.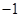 | B. | C.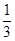 | D.1 |
函数 在x=1处取到极值,则a的值为( )
在x=1处取到极值,则a的值为( )
A. | B. | C.0 | D. |
函数 的递增区间是( )
的递增区间是( )
A. | B. | C. | D. |
设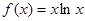 ,若
,若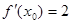 ,则
,则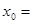 ( )
( )
A.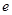 | B.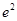 | C.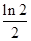 | D.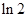 |
函数y=x4-4x+3在区间[-2,3]上的最小值为( )
| A.72 | B.36 | C.12 | D.0 |