题目内容
求下列函数的单调递减区间(1)
 ;
;(2)y=2x2-lnx.
【答案】分析:分别求导数,令其小于0,解不等式即可,注意和函数的定义域取交集.
解答:解:(1)求导数y′=3x2-x-2=(3x+2)(x-1)…(2分)
令y′<0,可解得 …(5分)
…(5分)
因此,原函数的减区间是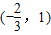 .…(6分)
.…(6分)
(2)原函数的定义域是(0,+∞),
求导数可得 …(8分)
…(8分)
令y′<0,可解得 ,…(11分)
,…(11分)
因此,原函数的减区间是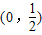 …(12分)
…(12分)
点评:本题考查函数的单调区间的求解,求导数并解不等式是解决问题的关键,属基础题.
解答:解:(1)求导数y′=3x2-x-2=(3x+2)(x-1)…(2分)
令y′<0,可解得
 …(5分)
…(5分)因此,原函数的减区间是
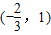 .…(6分)
.…(6分)(2)原函数的定义域是(0,+∞),
求导数可得
 …(8分)
…(8分)令y′<0,可解得
 ,…(11分)
,…(11分)因此,原函数的减区间是
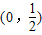 …(12分)
…(12分)点评:本题考查函数的单调区间的求解,求导数并解不等式是解决问题的关键,属基础题.

练习册系列答案
相关题目