题目内容
设椭圆![]() +y2=1的两个焦点是F1(-c,0)与F2(c,0),(c>0),且椭圆上存在一点P,使得直线PF1与PF2垂直.
+y2=1的两个焦点是F1(-c,0)与F2(c,0),(c>0),且椭圆上存在一点P,使得直线PF1与PF2垂直.
(1)求实数m的取值范围;
(2)设l是相应于焦点F2的准线,直线PF2与l相交于点Q,若|![]() |=2-
|=2-![]() ,求直线PF2的方程.
,求直线PF2的方程.
答案:
解析:
解析:
|
解:(1)由题设有m>0,c= 将①与 x02= 由m>0,x02= 所以m的取值范围是m≥1. (2)准线l的方程为x= 将x0= 由题设 将x0=- 由题设 解得m=2.从而x0=- 得到PF2的方程y=±( 分析:本小题主要考查直线和椭圆的基本知识,以及综合分析和解题能力. |

练习册系列答案
相关题目
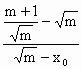 . ②
. ②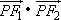 的值为
的值为
 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆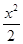 +y2=1有两个不同的交点P和Q.
+y2=1有两个不同的交点P和Q. +
+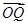 与
与 共线?如果存在,求k的值;如果不存在,请说明理由.
共线?如果存在,求k的值;如果不存在,请说明理由. +y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时,
+y2=1的两焦点,P在椭圆上,当△F1PF2面积为1时, 的值为 ( )
的值为 ( )