题目内容
(2011年高考全国卷理科)设向量
、
、
满足|
|=|
|=1,
•
=-
,<
-
,
-
>=600,则|
|的最大值等于( )
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| c |
| b |
| c |
| c |
分析:构造
=
,
=
,
=
,∠BAD=120°,∠BCD=60°,可得A,B,C,D四点共圆,且圆的半径等于1,
故当线段AC为直径时,|
|最大,最大值为圆的直径.
| AB |
| a |
| AD |
| b |
| AC |
| c |
故当线段AC为直径时,|
| c |
解答: 解:如图,由于|
解:如图,由于|
|=|
|=1,
•
=-
,<
-
,
-
>=600,
构造
=
,
=
,
=
,∠BAD=120°,∠BCD=60°,
所以A,B,C,D四点共圆.
由于BD=|
-
|=
=
=
,
△BCD中,由正弦定理可得 2R=
=
=2,
故四边形外接圆的半径等于1,
可知当线段AC为直径时,|
|最大,最大值为2.
故选A.
 解:如图,由于|
解:如图,由于|| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| c |
| b |
| c |
构造
| AB |
| a |
| AD |
| b |
| AC |
| c |
所以A,B,C,D四点共圆.
由于BD=|
| a |
| b |
(
|
|
| 3 |
△BCD中,由正弦定理可得 2R=
| BD |
| sin∠BCD |
| ||||
|
故四边形外接圆的半径等于1,
可知当线段AC为直径时,|
| c |
故选A.
点评:本题主要考查两个向量的数量积的运算,正弦定理,体现了数形结合的数学思想和等价转化的数学思想,
属于中档题.
属于中档题.

练习册系列答案
相关题目
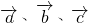 满足|
满足| |=|
|=| |=1,
|=1, =
= ,
,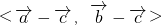 =600,则
=600,则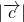 的最大值等于
的最大值等于

 满足|
满足| |=|
|=| |=1,
|=1, =
= ,
, =60,则
=60,则 的最大值等于( )
的最大值等于( )

 满足|
满足| |=|
|=| |=1,
|=1, =
= ,
, =60,则
=60,则 的最大值等于( )
的最大值等于( )

 满足|
满足| |=|
|=| |=1,
|=1, =
= ,
, =60,则
=60,则 的最大值等于( )
的最大值等于( )
