题目内容
若实数 满足
满足 ,
, 的取值范围为( ).
的取值范围为( ).
A. | B. | C. | D. |
A
解析试题分析:令 =t,即ty-x-4t+2=0,表示一条直线,又方程
=t,即ty-x-4t+2=0,表示一条直线,又方程 化为
化为 表示圆心为(1,1)半径为1的圆,由题意直线与圆有公共点,∴圆心(1,1)到直线ty-x-4t+2=0的距离
表示圆心为(1,1)半径为1的圆,由题意直线与圆有公共点,∴圆心(1,1)到直线ty-x-4t+2=0的距离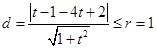 ,∴
,∴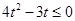 ,∴
,∴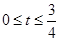 ,又t≠0,故
,又t≠0,故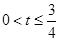 ,即
,即 的取值范围为,故选A
的取值范围为,故选A
考点:本题考查了直线与圆的位置关系
点评:此类问题常常结合式子的几何意义转化为直线与圆的位置关系问题,属基础题

练习册系列答案
相关题目
若直线 与圆
与圆 有公共点,则实数a取值范围是( )
有公共点,则实数a取值范围是( )
| A.[-3,-1] | B.[-1,3] |
| C.[-3,l ] | D.(-∞,-3]  [1.+∞) [1.+∞) |
下列满足“与直线 平行,且与圆
平行,且与圆 相切”的是( )
相切”的是( )
A.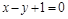 | B. |
C. | D. |
已知圆O: ,直线
,直线 过点
过点 ,且与直线OP垂直,则直线
,且与直线OP垂直,则直线 的方程为( )
的方程为( )
A. | B. | C. | D. |
若函数 的图象在
的图象在 处的切线
处的切线 与圆
与圆 相离,则点
相离,则点 与圆C的位置关系是 ( )
与圆C的位置关系是 ( )
| A.点在圆外 | B.点在圆内 | C.点在圆上 | D.不能确定 |
若过定点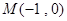 且斜率为
且斜率为 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则 的取值范围是( ).
的取值范围是( ).
A. | B.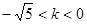 |
C. | D. |
若直线 截得的弦最短,则直线
截得的弦最短,则直线 的方程是
的方程是
A. | B. |
C. | D. |
 中,圆
中,圆 的方程为
的方程为 ,若直线
,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 的取值范围是( )
的取值范围是( )
 或
或
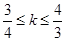
 或
或 ,则直线倾斜角的取值范围是( )
,则直线倾斜角的取值范围是( )


