题目内容
设y=2x2+2ax+b(x∈R),已知当 时y有最小值-8.
时y有最小值-8.
(1)试求不等式y>0的解集;
(2)集合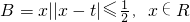 ,且A∩B=∅,确定实数t的取值范围.
,且A∩B=∅,确定实数t的取值范围.
解:(1)由当 时y有最小值-8
时y有最小值-8
得:y=2(x- )2-8
)2-8
可化为:y=2x2-x-
不等式y>0即2(x- )2-8>0.
)2-8>0.
解得:x> 或x<-
或x<-
(2)∵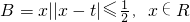 ={x|t-
={x|t- ≤x≤t+
≤x≤t+ }
}
因为A∩B=∅,所以得到: ,
,
解得:-1≤t≤2,
所以是实数t的取值范围是:[1,2].
分析:(1)由当 时y有最小值-8得出函数的解析式,即:y=2(x-
时y有最小值-8得出函数的解析式,即:y=2(x- )2-8,再结合一元二次不等式求解即得;
)2-8,再结合一元二次不等式求解即得;
(2)由(1)得集合A,再求出和B中不等式的解集,根据两集合的交集为空集,列出关于t的不等式组,求出不等式组的解集即可得到t的取值范围.
点评:此题要求学生掌握交集、空集的定义及性质,是一道基础题.
 时y有最小值-8
时y有最小值-8得:y=2(x-
 )2-8
)2-8可化为:y=2x2-x-

不等式y>0即2(x-
 )2-8>0.
)2-8>0.解得:x>
 或x<-
或x<-
(2)∵
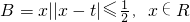 ={x|t-
={x|t- ≤x≤t+
≤x≤t+ }
}因为A∩B=∅,所以得到:
 ,
,解得:-1≤t≤2,
所以是实数t的取值范围是:[1,2].
分析:(1)由当
 时y有最小值-8得出函数的解析式,即:y=2(x-
时y有最小值-8得出函数的解析式,即:y=2(x- )2-8,再结合一元二次不等式求解即得;
)2-8,再结合一元二次不等式求解即得;(2)由(1)得集合A,再求出和B中不等式的解集,根据两集合的交集为空集,列出关于t的不等式组,求出不等式组的解集即可得到t的取值范围.
点评:此题要求学生掌握交集、空集的定义及性质,是一道基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目