题目内容
设y=2x2+2ax+b(x∈R),已知当x=
时y有最小值-8.
(1)试求不等式y>0的解集;
(2)集合B={x||x-t|≤
,x∈R},且A∩B=∅,确定实数t的取值范围.
| 1 |
| 2 |
(1)试求不等式y>0的解集;
(2)集合B={x||x-t|≤
| 1 |
| 2 |
(1)由当x=
时y有最小值-8
得:y=2(x-
)2-8
可化为:y=2x2-x-
不等式y>0即2(x-
)2-8>0.
解得:x>
或x<-
(2)∵B={x||x-t|≤
,x∈R}={x|t-
≤x≤t+
}
因为A∩B=∅,所以得到:
,
解得:-1≤t≤2,
所以是实数t的取值范围是:[1,2].
| 1 |
| 2 |
得:y=2(x-
| 1 |
| 2 |
可化为:y=2x2-x-
| 15 |
| 2 |
不等式y>0即2(x-
| 1 |
| 2 |
解得:x>
| 5 |
| 2 |
| 3 |
| 2 |
(2)∵B={x||x-t|≤
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为A∩B=∅,所以得到:
|
解得:-1≤t≤2,
所以是实数t的取值范围是:[1,2].

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 时y有最小值-8.
时y有最小值-8.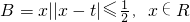 ,且A∩B=∅,确定实数t的取值范围.
,且A∩B=∅,确定实数t的取值范围.