题目内容
过抛物线x2=2py(p>0)的焦点F作直线l1交抛物线于A、B两点.O为坐标原点.(1)过点A作抛物线的切线交y轴于点C,求线段AC中点M的轨迹方程;
(2)若l1倾斜角为30°,则在抛物线准线l2上是否存在点E,使得△ABE为正三角形,若存在,求出E点坐标,若不存在,说明理由.
【答案】分析:(1)先设出过点A的抛物线的切线方程,与抛物线方程联立,利用△=0,求出k,再代回切线方程,求C点坐标,这样就可找到AC中点的坐标,进而求出中点M的轨迹方程.
(2)假设存在符合题意的点E.由已知l1:y-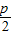 =
=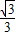 x 联立抛物线方程有:x2=2p(
x 联立抛物线方程有:x2=2p(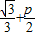 ),故可求A,B的坐标.欲使△ABE为正△,则kBE不存在.从而可知不存在符合条件的点E.
),故可求A,B的坐标.欲使△ABE为正△,则kBE不存在.从而可知不存在符合条件的点E.
解答:解:(1)设A(x1,y1),过点A的切线方程为y=k(x-x1)+y1
由 得x2-2pkx+2pkx1-2py1=0
得x2-2pkx+2pkx1-2py1=0
令△=4p2k2-4(2pkx1-2py1)=0
解得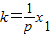
∴切线方程为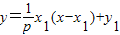
令x=0,得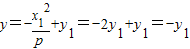
∴线段AC中点M为(x,0)
∴点M的轨迹方程为y=0(x≠0)
(2)假设存在符合题意的点E.
由已知l1:y-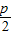 =
= x 联立抛物线方程有:x2=2p(
x 联立抛物线方程有:x2=2p(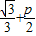 )
)
∴x2-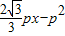 =0
=0
∴x1=-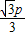 ,x2=
,x2=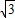 p
p
故A(-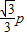 ,
,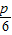 ),B(
),B(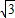 p,
p, p)
p)
∵△ABE为正△
∴kAE=-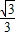
∴AE:y-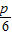 =-
=-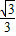 (x+
(x+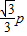 ) 即y=-
) 即y=-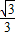 x-
x-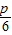
准线l2:y=- ∴E(-
∴E(-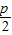 ,
,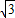 p)
p)
欲使△ABE为正△,则kBE不存在.即xB=xE不符合
∴不存在符合条件的点E.
点评:本题以抛物线为载体,考查直线与抛物线的位置关系,解题的关键是直线与抛物线方程联立,转化为一元二次方程求解.
(2)假设存在符合题意的点E.由已知l1:y-
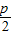 =
=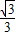 x 联立抛物线方程有:x2=2p(
x 联立抛物线方程有:x2=2p(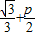 ),故可求A,B的坐标.欲使△ABE为正△,则kBE不存在.从而可知不存在符合条件的点E.
),故可求A,B的坐标.欲使△ABE为正△,则kBE不存在.从而可知不存在符合条件的点E.解答:解:(1)设A(x1,y1),过点A的切线方程为y=k(x-x1)+y1
由
 得x2-2pkx+2pkx1-2py1=0
得x2-2pkx+2pkx1-2py1=0令△=4p2k2-4(2pkx1-2py1)=0
解得
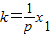
∴切线方程为
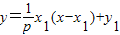
令x=0,得
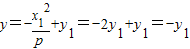
∴线段AC中点M为(x,0)
∴点M的轨迹方程为y=0(x≠0)
(2)假设存在符合题意的点E.
由已知l1:y-
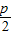 =
= x 联立抛物线方程有:x2=2p(
x 联立抛物线方程有:x2=2p(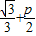 )
)∴x2-
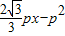 =0
=0∴x1=-
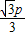 ,x2=
,x2=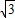 p
p 故A(-
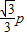 ,
,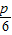 ),B(
),B(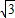 p,
p, p)
p)∵△ABE为正△
∴kAE=-
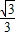
∴AE:y-
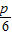 =-
=-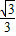 (x+
(x+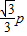 ) 即y=-
) 即y=-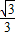 x-
x-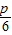
准线l2:y=-
 ∴E(-
∴E(-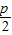 ,
,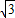 p)
p)欲使△ABE为正△,则kBE不存在.即xB=xE不符合
∴不存在符合条件的点E.
点评:本题以抛物线为载体,考查直线与抛物线的位置关系,解题的关键是直线与抛物线方程联立,转化为一元二次方程求解.

练习册系列答案
相关题目
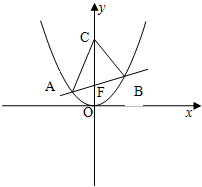 设直线l过抛物线x2=2py(p>0)的焦点F,且与该抛物线交于A、B两点,l的斜率为k,点C(0,t),当k=0,t=1+2
设直线l过抛物线x2=2py(p>0)的焦点F,且与该抛物线交于A、B两点,l的斜率为k,点C(0,t),当k=0,t=1+2