题目内容
已知双曲线方程 ,椭圆方程
,椭圆方程 ,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,|OC|,|OD|成等比数列.
,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,|OC|,|OD|成等比数列.(Ⅰ)求椭圆的方程;
(Ⅱ)若E是椭圆长轴的左端点,动点M满足MC⊥CE,连接EM,交椭圆于点P,在x轴上有异于点E的定点Q,使得以MP为直径的圆恒过直线CP、MQ的交点,求点Q的坐标.
【答案】分析:(Ⅰ)由双曲线方程 ,可求
,可求 ,根据|OA|,|OB|,|OC|,|OD|成等比数列,可得
,根据|OA|,|OB|,|OC|,|OD|成等比数列,可得 ,根据D是椭圆的右准线与x轴的交点,C为椭圆的右顶点,即可求得椭圆的方程;
,根据D是椭圆的右准线与x轴的交点,C为椭圆的右顶点,即可求得椭圆的方程;
(Ⅱ)由(Ⅰ)知,C(2,0),E(-2,0),将y=k(x+2)代入 整理得(1+2k2)x2+8k2x+8k2-4=0,可求P的坐标;设Q(x,0),x≠-2,若以MP为直径的圆恒过直线CP、MQ的交点,则MQ⊥CP,从而有
整理得(1+2k2)x2+8k2x+8k2-4=0,可求P的坐标;设Q(x,0),x≠-2,若以MP为直径的圆恒过直线CP、MQ的交点,则MQ⊥CP,从而有 ,进而可知存在Q(0,0),使得以MP为直径的圆恒过直线CP、MQ的交点.
,进而可知存在Q(0,0),使得以MP为直径的圆恒过直线CP、MQ的交点.
解答:解:(Ⅰ)由已知A是双曲线的右准线与x轴的交点,B为双曲线的右顶点,双曲线方程 ,
,
∴
∵|OA|,|OB|,|OC|,|OD|成等比数列.
∴
∵D是椭圆的右准线与x轴的交点,C为椭圆的右顶点,
∴
∴
∴所求椭圆的方程为 ;
;
(Ⅱ)由(Ⅰ)知,C(2,0),E(-2,0),设直线EM的方程为:y=k(x+2),P(x1,y1)
∵MC⊥CE,∴M(2,4k)
将y=k(x+2)代入 整理得(1+2k2)x2+8k2x+8k2-4=0
整理得(1+2k2)x2+8k2x+8k2-4=0
∵
∴
∴
∴P( )
)
设Q(x,0),x≠-2
若以MP为直径的圆恒过直线CP、MQ的交点,则MQ⊥CP
∴
∵ ,
,
∴ =0
=0
∴
∴x=0
∴存在Q(0,0),使得以MP为直径的圆恒过直线CP、MQ的交点.
点评:本题重点考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是将两直线与椭圆方程联立,将向量关系转化为坐标关系.
 ,可求
,可求 ,根据|OA|,|OB|,|OC|,|OD|成等比数列,可得
,根据|OA|,|OB|,|OC|,|OD|成等比数列,可得 ,根据D是椭圆的右准线与x轴的交点,C为椭圆的右顶点,即可求得椭圆的方程;
,根据D是椭圆的右准线与x轴的交点,C为椭圆的右顶点,即可求得椭圆的方程;(Ⅱ)由(Ⅰ)知,C(2,0),E(-2,0),将y=k(x+2)代入
 整理得(1+2k2)x2+8k2x+8k2-4=0,可求P的坐标;设Q(x,0),x≠-2,若以MP为直径的圆恒过直线CP、MQ的交点,则MQ⊥CP,从而有
整理得(1+2k2)x2+8k2x+8k2-4=0,可求P的坐标;设Q(x,0),x≠-2,若以MP为直径的圆恒过直线CP、MQ的交点,则MQ⊥CP,从而有 ,进而可知存在Q(0,0),使得以MP为直径的圆恒过直线CP、MQ的交点.
,进而可知存在Q(0,0),使得以MP为直径的圆恒过直线CP、MQ的交点.解答:解:(Ⅰ)由已知A是双曲线的右准线与x轴的交点,B为双曲线的右顶点,双曲线方程
 ,
,∴

∵|OA|,|OB|,|OC|,|OD|成等比数列.
∴

∵D是椭圆的右准线与x轴的交点,C为椭圆的右顶点,
∴

∴

∴所求椭圆的方程为
 ;
;(Ⅱ)由(Ⅰ)知,C(2,0),E(-2,0),设直线EM的方程为:y=k(x+2),P(x1,y1)
∵MC⊥CE,∴M(2,4k)
将y=k(x+2)代入
 整理得(1+2k2)x2+8k2x+8k2-4=0
整理得(1+2k2)x2+8k2x+8k2-4=0∵

∴

∴

∴P(
 )
)设Q(x,0),x≠-2
若以MP为直径的圆恒过直线CP、MQ的交点,则MQ⊥CP
∴

∵
 ,
,
∴
 =0
=0∴

∴x=0
∴存在Q(0,0),使得以MP为直径的圆恒过直线CP、MQ的交点.
点评:本题重点考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,解题的关键是将两直线与椭圆方程联立,将向量关系转化为坐标关系.

练习册系列答案
相关题目
 ,椭圆方程
,椭圆方程 ,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,
,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,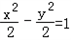 ,椭圆方程
,椭圆方程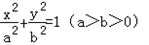 ,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,
,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|, ,椭圆方程
,椭圆方程 ,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,|OC|,|OD|成等比数列.
,A、D分别是双曲线和椭圆的右准线与x轴的交点,B、C分别为双曲线和椭圆的右顶点,O为坐标原点,且|OA|,|OB|,|OC|,|OD|成等比数列.