题目内容
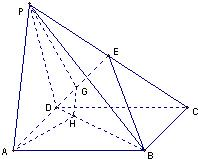17、如图，点P为平行四边形ABCD所在平面外一点，点E为PC的中点，在DE上取一点G，过点G和直线AP作平面APG交平面BDE于GH，求证：AP∥GH．分析：如图，要证明AP∥GH，连接AC交BD于一点O，连接OE，
容易证明OE∥AP，则AP∥平面BDE，又过AP的平面交平面
BDE于直线GH，由线面平行的性质定理及公理三可证之．
容易证明OE∥AP，则AP∥平面BDE，又过AP的平面交平面
BDE于直线GH，由线面平行的性质定理及公理三可证之．
解答：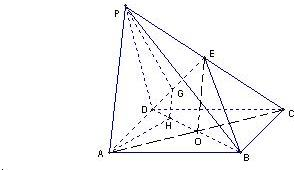
证明：连接AC交BD于点O，连接OE，则OE∥AP．
又∵OE?平面DEB，PA?平面DEB
∴AP∥平面BDE又∵平面APGH∩平面DEB=GH，
∴AP∥GH．
证明：连接AC交BD于点O，连接OE，则OE∥AP．又∵OE?平面DEB，PA?平面DEB
∴AP∥平面BDE又∵平面APGH∩平面DEB=GH，
∴AP∥GH．
点评：本题考查线线平行的定理，由公理三，需要证明两条直线与第三条直线平行，而本题条件易证线面平行，再由性质定理可得．注意转化思想的应用．
练习册系列答案
相关题目
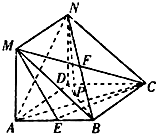如图，MA⊥平面ABCD，四边形ABCD是菱形，四边开ADNM是平行四边形．