题目内容
函数y=f(x)=x3+ax2+bx+a2,在x=1时,有极值10,则a= ,b= .
【答案】分析:由f′(1)=0与f(1)=10即可建立方程求得a,b的值.
解答:解:∵函数y=f(x)=x3+ax2+bx+a2,
∴f′(x)=3x2+2ax+b,
又x=1时,有极值10,
∴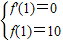 ,即
,即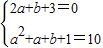 ,解得
,解得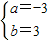 或
或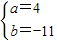 .
.
若a=-3,b=3,f′(x)=3x2-6x+3=3(x-1)2≥0恒成立,y=f(x)在R上单调递增,无极值,故舍去;
若a=4,b=-11,f′(x)=3x2+8x-11=(x-1)(3x+11),经检验满足题意.
故a=4,b=-11.
故答案为:4,-11.
点评:本题考查利用导数研究函数的极值,考查方程思想与分类讨论思想及分析推理与运算能力,属于中档题.
解答:解:∵函数y=f(x)=x3+ax2+bx+a2,
∴f′(x)=3x2+2ax+b,
又x=1时,有极值10,
∴
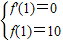 ,即
,即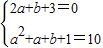 ,解得
,解得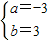 或
或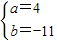 .
.若a=-3,b=3,f′(x)=3x2-6x+3=3(x-1)2≥0恒成立,y=f(x)在R上单调递增,无极值,故舍去;
若a=4,b=-11,f′(x)=3x2+8x-11=(x-1)(3x+11),经检验满足题意.
故a=4,b=-11.
故答案为:4,-11.
点评:本题考查利用导数研究函数的极值,考查方程思想与分类讨论思想及分析推理与运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目