题目内容
(2006年广东卷)设函数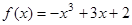 分别在
分别在 、
、 处取得极小值、极大值.
处取得极小值、极大值. 平面上点A、B的坐标分别为
平面上点A、B的坐标分别为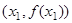 、
、 ,该平面上动点P满足
,该平面上动点P满足 ,点Q是点P关于直线
,点Q是点P关于直线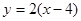 的对称点
的对称点
求:(Ⅰ)点A、B的坐标 ;
(Ⅱ)动点Q的轨迹方程
【答案】
(Ⅰ) 点A、B的坐标为 .(Ⅱ)
.(Ⅱ) 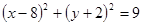
【解析】
试题分析:分析:根据极值点得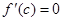 ,根据附近导数判断极小值、极大值点;根据向量的数量及对称点坐标关系可求得Q点轨迹.
,根据附近导数判断极小值、极大值点;根据向量的数量及对称点坐标关系可求得Q点轨迹.
解: (Ⅰ)令 解得
解得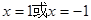
当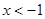 时,
时,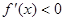 ,
当
,
当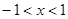 时,
时,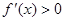 ,当
,当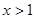 时,
时,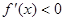
所以,函数在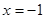 处取得极小值,在
处取得极小值,在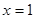 取得极大值,故
取得极大值,故
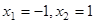 ,
,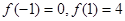
所以, 点A、B的坐标为 .
.
(Ⅱ) 设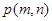 ,
,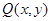 ,
,
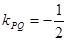 ,所以
,所以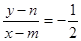 ,又PQ的中点在
,又PQ的中点在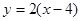 上,所以
上,所以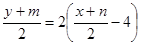
消去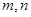 得
得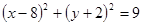
考点:本题主要考查向量数量积、导数的应用。
点评:本题主要考查了向量和导数的结合,(2)中求轨迹方程,使用了“相关点法”.

练习册系列答案
相关题目
 的展开式中,x5的系数为 .
的展开式中,x5的系数为 .