题目内容
(2006年广东卷)在 的展开式中,x5的系数为 .
的展开式中,x5的系数为 .
【答案】分析:根据题意,由二项式定理可得 的通项,进而可得含x5的为第4项,由通项求出第4项即可得答案.
的通项,进而可得含x5的为第4项,由通项求出第4项即可得答案.
解答:解:由二项式定理可得 的通项为Tr+1=C11r(x)11-r(-
的通项为Tr+1=C11r(x)11-r(- )r=(-1)rC11rx11-2r2r,
)r=(-1)rC11rx11-2r2r,
11-2r=5,解可得r=3,则含x5的为第4项,
T4=(-1)3C113(x)5(2)3=-1320x5,
即x5的系数为-1320,
故答案为-1320.
点评:本题考查二项式定理,解题的关键在于牢记二项式的通项公式,同时分清二项式系数与某一项的系数两个概念.
 的通项,进而可得含x5的为第4项,由通项求出第4项即可得答案.
的通项,进而可得含x5的为第4项,由通项求出第4项即可得答案.解答:解:由二项式定理可得
 的通项为Tr+1=C11r(x)11-r(-
的通项为Tr+1=C11r(x)11-r(- )r=(-1)rC11rx11-2r2r,
)r=(-1)rC11rx11-2r2r,11-2r=5,解可得r=3,则含x5的为第4项,
T4=(-1)3C113(x)5(2)3=-1320x5,
即x5的系数为-1320,
故答案为-1320.
点评:本题考查二项式定理,解题的关键在于牢记二项式的通项公式,同时分清二项式系数与某一项的系数两个概念.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
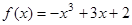 分别在
分别在 、
、 处取得极小值、极大值.
处取得极小值、极大值. 平面上点A、B的坐标分别为
平面上点A、B的坐标分别为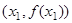 、
、 ,该平面上动点P满足
,该平面上动点P满足 ,点Q是点P关于直线
,点Q是点P关于直线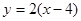 的对称点
的对称点