题目内容
设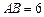 ,在线段
,在线段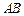 上任取两点C,D(端点
上任取两点C,D(端点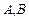 除外),将线段
除外),将线段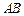 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
(X是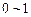 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是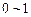 之间的均匀随机
之间的均匀随机 数)
数)
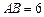 ,在线段
,在线段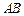 上任取两点C,D(端点
上任取两点C,D(端点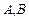 除外),将线段
除外),将线段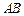 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
| | 1组 | 2组 | 3组 | 4组 | 5组 | 6组 | 7组 | 8组 | 9组 | 10组 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0. 6 6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0 .86 .86 |
| | 11组 | 12组 | 13组 | 14组 | 15组 | 16组 | 17组 | 18组 | 19组 | 20组 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0. 64 64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
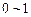 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是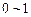 之间的均匀随机
之间的均匀随机 数)
数)解:(1)所有的基本事件有:(1,1,4),(1,2,3),(1,3,2),(1,4,1),(2,1,3),(2,2,2),(2,3,1),(3,1,2),(3,2,1),(4 ,1,1),其中(a,b,c)表示所分成三条线段的长度,共有10种.
,1,1),其中(a,b,c)表示所分成三条线段的长度,共有10种.
而事件A所包含的基本事件为(2,2,2 ),共1种.
),共1种.
故
 , 所以所分成的三条线段可以构成三角形的概率为
, 所以所分成的三条线段可以构成三角形的概率为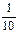 .
.
(2)设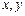 为分成三条线段中的两条长度.
为分成三条线段中的两条长度. 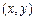 可以看成平面中的点,试验的全部结果所构成的区域为
可以看成平面中的点,试验的全部结果所构成的区域为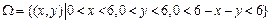 ,如图所示,其面积为
,如图所示,其面积为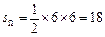 ,事件B所构成的区域为
,事件B所构成的区域为

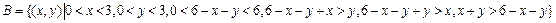 如图所示阴影部分,其面积为
如图所示阴影部分,其面积为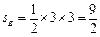 ,故
,故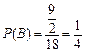
所以这三条线段可以构成三角形的概率为
(3)步骤如下:
①产生两组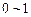 之间的均匀随机数X、Y(题目给出)
之间的均匀随机数X、Y(题目给出)
②经平移和伸缩变换,
③数出落在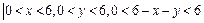 的点
的点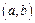 的个数N和落在
的个数N和落在

的点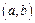 的个数N1,由已知中的20组随机数可数得N=13,N1=3
的个数N1,由已知中的20组随机数可数得N=13,N1=3
④由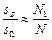 计算得:
计算得: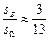 ,故
,故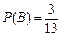
 ,1,1),其中(a,b,c)表示所分成三条线段的长度,共有10种.
,1,1),其中(a,b,c)表示所分成三条线段的长度,共有10种.而事件A所包含的基本事件为(2,2,2
 ),共1种.
),共1种.故

 , 所以所分成的三条线段可以构成三角形的概率为
, 所以所分成的三条线段可以构成三角形的概率为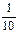 .
. (2)设
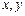 为分成三条线段中的两条长度.
为分成三条线段中的两条长度. 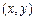 可以看成平面中的点,试验的全部结果所构成的区域为
可以看成平面中的点,试验的全部结果所构成的区域为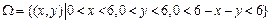 ,如图所示,其面积为
,如图所示,其面积为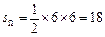 ,事件B所构成的区域为
,事件B所构成的区域为
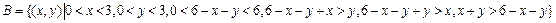 如图所示阴影部分,其面积为
如图所示阴影部分,其面积为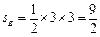 ,故
,故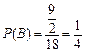
所以这三条线段可以构成三角形的概率为

(3)步骤如下:
①产生两组
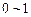 之间的均匀随机数X、Y(题目给出)
之间的均匀随机数X、Y(题目给出)②经平移和伸缩变换,

③数出落在
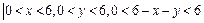 的点
的点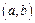 的个数N和落在
的个数N和落在
的点
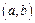 的个数N1,由已知中的20组随机数可数得N=13,N1=3
的个数N1,由已知中的20组随机数可数得N=13,N1=3④由
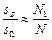 计算得:
计算得: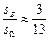 ,故
,故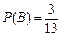
略

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.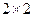 列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系? ,
,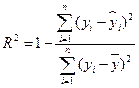 ,可能用到数据:
,可能用到数据: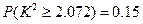 ,
,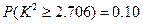 ,
,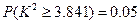 ,
,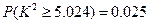 .)
.) 必过点( )
必过点( )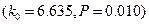
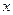 ,数学成绩为
,数学成绩为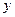 (注:没有相同姓名的学生).
(注:没有相同姓名的学生).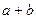 的值;
的值; 的概率;
的概率;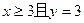 的概率.
的概率.
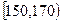 内的学
内的学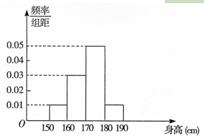
 试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表: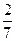
 绩与班级有关系”。
绩与班级有关系”。 分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
分)有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表
 观测值的计算式
观测值的计算式 有关?
有关? )
) 0.100,P(k
0.100,P(k )
) /100kg)与上市时间
/100kg)与上市时间 (单位:天)的数据如下表:
(单位:天)的数据如下表: 250
250



