题目内容
在平面直角坐标系内,设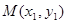 、
、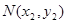 为不同的两点,直线
为不同的两点,直线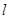 的方程为
的方程为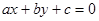 , 设
, 设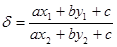 有下列四个说法:
有下列四个说法:
①存在实数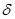 ,使点
,使点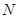 在直线
在直线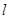 上;
上;
②若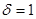 ,则过
,则过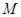 、
、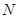 两点的直线与直线
两点的直线与直线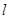 平行;
平行;
③若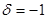 ,则直线
,则直线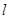 经过线段
经过线段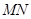 的中点;
的中点;
④若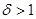 ,则点
,则点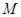 、
、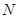 在直线
在直线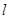 的同侧,且直线
的同侧,且直线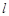 与线段
与线段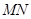 的延长线相交
的延长线相交
上述说法中,所有正确说法的序号是
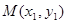 、
、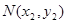 为不同的两点,直线
为不同的两点,直线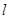 的方程为
的方程为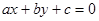 , 设
, 设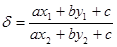 有下列四个说法:
有下列四个说法:①存在实数
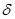 ,使点
,使点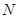 在直线
在直线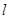 上;
上;②若
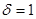 ,则过
,则过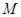 、
、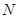 两点的直线与直线
两点的直线与直线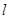 平行;
平行;③若
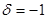 ,则直线
,则直线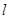 经过线段
经过线段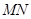 的中点;
的中点;④若
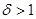 ,则点
,则点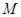 、
、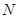 在直线
在直线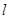 的同侧,且直线
的同侧,且直线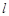 与线段
与线段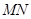 的延长线相交
的延长线相交 上述说法中,所有正确说法的序号是
②③④
试题分析:若点
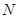 在直线
在直线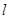 上,即满足
上,即满足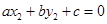 所以不存在这样的实数
所以不存在这样的实数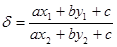 所以①不正确;若
所以①不正确;若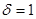 ,即
,即 ,所以
,所以 即
即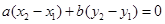 所以
所以 即过
即过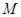 、
、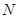 两点的直线与直线
两点的直线与直线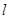 平行成立 所以②正确;若
平行成立 所以②正确;若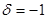 即
即 把线段
把线段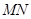 的中点代入直线
的中点代入直线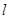 即可得,所以③正确;若
即可得,所以③正确;若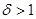 即
即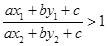 ,所以
,所以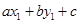 与
与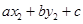 的值同正或同负,即点
的值同正或同负,即点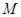 、
、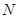 在直线
在直线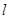 的同侧,又因为
的同侧,又因为 >
>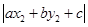 所以点N离直线
所以点N离直线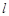 更近,所以直线
更近,所以直线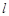 与线段
与线段 的延长线相交 所以④正确 综上填②③④
的延长线相交 所以④正确 综上填②③④
练习册系列答案
相关题目
 ,且直线L在x轴上的截距等于在y轴上的截距的2倍,求直线L的方程.
,且直线L在x轴上的截距等于在y轴上的截距的2倍,求直线L的方程.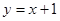 ,则AC所在的直线方程为( )
,则AC所在的直线方程为( )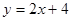

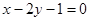
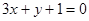
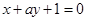 与直线
与直线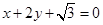 平行,则实数
平行,则实数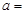 ( )
( )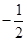
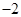
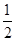
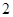
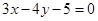 与两坐标轴围成的三角形面积等于__________.
与两坐标轴围成的三角形面积等于__________.