题目内容
如图,在平面直角坐标系 中,点
中,点 ,直线
,直线 。设圆
。设圆 的半径为
的半径为 ,圆心在
,圆心在 上。
上。
(1)若圆心 也在直线
也在直线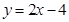 上,过点
上,过点 作圆
作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围。
的取值范围。
(1) 或
或 ;(2)
;(2) .
.
解析试题分析:(1)由题设点 ,又
,又 也在直线
也在直线 上,点
上,点 满足直线
满足直线 的方程,从而求出圆的方程,可将切线方程可设为
的方程,从而求出圆的方程,可将切线方程可设为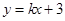 ,则圆心到切线的距离等于圆的半径,即可求出切线的方程;(2)设点
,则圆心到切线的距离等于圆的半径,即可求出切线的方程;(2)设点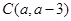 ,
, ,
, ,
, ,
, ,
, 即
即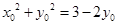 ,又点
,又点 在圆
在圆 上,
上, ,
, 点为
点为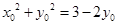 与
与 的交点,
的交点,
若存在这样的点 ,则
,则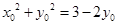 与
与 有交点,
有交点,
即圆心之间的距离 满足:
满足: ,从而求出
,从而求出 的取值范围.
的取值范围.
试题解析:(1)由题设点 ,又
,又 也在直线
也在直线 上,
上,
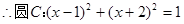 ,由题,过A点切线方程可设为
,由题,过A点切线方程可设为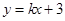 ,
,
即 ,则
,则 ,解得:
,解得: ,
,
又当斜率不存在时,也与圆相切,∴所求切线为 或
或 ,
,
即 或
或
(2)设点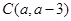 ,
, ,
, ,
, ,
, ,
, 即
即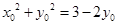 ,又点
,又点 在圆
在圆 上,
上, ,
, 点为
点为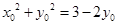 与
与 的交点,
的交点,
若存在这样的点 ,则
,则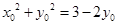 与
与 有交点,
有交点,
即圆心之间的距离 满足:
满足: ,
, 即
即 ,
,
解得:
考点:本题主要考查了圆的标准方程,直线与圆的位置关系,圆与圆的位置关系,以及两点间的距离公式,解题的关键是抓住直线与圆,圆与圆的位置关系.

练习册系列答案
相关题目
 ,
, ,若存在实数
,若存在实数 ,使得
,使得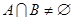 ,则实数
,则实数 的取值范围是___________.
的取值范围是___________. 在圆
在圆 上,点
上,点 关于直线
关于直线 的对称点也在圆
的对称点也在圆 上,则
上,则 。
。 .则直线
.则直线 被圆
被圆
 所截得的弦长为 .
所截得的弦长为 .  ,则直线
,则直线 被圆
被圆 所截得的弦长为 .
所截得的弦长为 . 的圆心是直线
的圆心是直线 与
与 轴的交点,且圆
轴的交点,且圆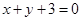 相切.则圆
相切.则圆 的最短路程是_________.
的最短路程是_________. 上,则圆C2的半径的最大值是________.
上,则圆C2的半径的最大值是________.