题目内容
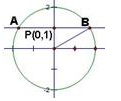
过点(0,1)的直线与x2+y2=4相交于A、B两点,则|AB|的最小值为________.
2
解析试题分析:要求解直线与圆相交时的弦长,那么结合图像,要使得|AB|的长度最小,那么就是求解半弦长最小时的情况。利用圆的半径和半弦长和弦心距的关系可知, 半径的平方等于弦心距的平方加上半弦长的平方得到。由于半径由x2+y2=4可知为2.只要满足圆心(0,0)到过点(0,1)的直线的距离最大即可,那么即为过点(0,1)且与圆心的连线垂直的直线,如图所示,那么此时的弦心距为1,那么利用上述的勾股定理可知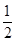 |AB|=
|AB|=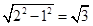 ,故|AB|的最小值为2
,故|AB|的最小值为2 ,故答案为2
,故答案为2 。
。
考点:本试题主要是考查了直线与圆的位置关系,计算弦心距,再求半弦长,得出结论.
点评:数形结合解答本题,它是选择题可以口算、心算、甚至不算,得出结果最好.

练习册系列答案
相关题目
 与曲线
与曲线 有四个不同的交点,则实数
有四个不同的交点,则实数 的取值范围是 。
的取值范围是 。 轴上,且过两点A(1,4),B(3,2)的圆的方程为 .
轴上,且过两点A(1,4),B(3,2)的圆的方程为 . ,若直线
,若直线 与
与 轴相交于点
轴相交于点 ,与
,与 轴相交于
轴相交于 ,且
,且 与圆
与圆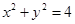 相交所得弦的长为2,
相交所得弦的长为2, 为坐标原点,则
为坐标原点,则 面积的最小值为_________.
面积的最小值为_________. 关于直线
关于直线 的对称圆方程是 .
的对称圆方程是 . 
 被圆
被圆 截得的弦长为4,则
截得的弦长为4,则 的最大值是 .
的最大值是 .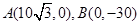 ,一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为 秒.
,一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为 秒.
 和圆
和圆 交于
交于 两点,且
两点,且 , 则
, 则  _______。
_______。 ,点
,点 是直线
是直线 上的一动点,当
上的一动点,当 最大时,则过
最大时,则过 的圆的方程是
的圆的方程是