题目内容
(本题14分,第(1)小题6分,第(2)小题8分)
已知函数![]() 的定义域为
的定义域为![]() (
(![]() 为常数).
为常数).
(1)证明:当![]() 时,函数
时,函数![]() 在定义域上是减函数;
在定义域上是减函数;
(2)求函数![]() 在定义域上的最大值及最小值,并求出函数取最值时
在定义域上的最大值及最小值,并求出函数取最值时![]() 的值.
的值.
(1)![]()
![]() 因为
因为![]()
所以![]()
![]()
所以![]() 是减函数
是减函数
(2)①当![]() ,
,![]() 是增函数
是增函数
所以![]() ,无最小值
,无最小值
②当![]() 时,
时,![]() 是增函数
是增函数
所以![]() ,无最小值
,无最小值
③当![]() 且
且![]() 即
即![]() 时,所以
时,所以![]() ,无最大值
,无最大值
④当![]() 且
且![]() 即
即![]() 时
时
所以![]() ,无最大值
,无最大值

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
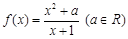 .
. 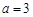 时,函数
时,函数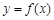 在
在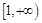 上是增函数;[来源:学.科.网Z.X.X.K]
上是增函数;[来源:学.科.网Z.X.X.K]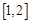 上有最小值
上有最小值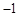 ,求实数
,求实数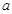 的值.
的值. .
. 的值;
的值; ,
, ,求
,求 的值.
的值. ,若不等式
,若不等式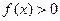 的解集为
的解集为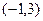 。
。 (1)求
(1)求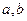 的值;
的值; 在
在 上的最小值为1,求实数
上的最小值为1,求实数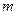 的值。
的值。