题目内容
本题14分,第(1)小题6分,第(2)小题8分)
已知函数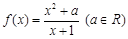 .
.
(1)用定义证明:当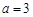 时,函数
时,函数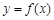 在
在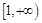 上是增函数;[来源:学.科.网Z.X.X.K]
上是增函数;[来源:学.科.网Z.X.X.K]
(2)若函数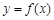 在
在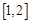 上有最小值
上有最小值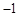 ,求实数
,求实数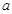 的值.
的值.
【答案】
(1)当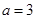 时,
时,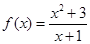
任取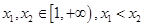 时,
时,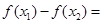
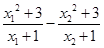

因为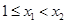 ,所以
,所以

所以 ,所以
,所以 在
在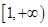 上为增函数。
上为增函数。
(2)解法一、根据题意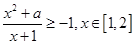 恒成立。且等号成立。
恒成立。且等号成立。
所以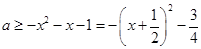
由于 在
在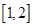 上单调递减,所以
上单调递减,所以
所以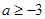 ;
;
当等式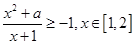 等号成立时,
等号成立时,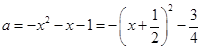
所以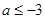 ,
,
故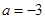
解法二、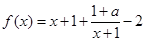 ,令
,令 ,则
,则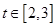


①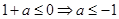 时,根据反比例函数与正比例函数的性质,
时,根据反比例函数与正比例函数的性质,
 为增函数
为增函数
所以 ,即:
,即: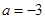
②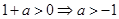 ,由于
,由于 ,所以
,所以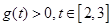 ,即
,即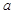 不存在。
不存在。
【解析】略

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 .
. 的值;
的值; ,
, ,求
,求 的值.
的值. ,若不等式
,若不等式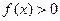 的解集为
的解集为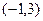 。
。 (1)求
(1)求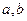 的值;
的值; 在
在 上的最小值为1,求实数
上的最小值为1,求实数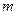 的值。
的值。