题目内容
在各项为正的数列{an}中,数列的前n项和Sn满足Sn=| 1 |
| 2 |
| 1 |
| an |
(1)求a1,a2,a3;
(2)由(1)猜想数列{an}的通项公式,并用数学归纳法证明你的猜想.
分析:(1)由题设条件,分别令n=1,2,3,能够求出a1,a2,a3.
(2)由(1)猜想数列{an}的通项公式:an=
-
(n∈N*),检验n=1时等式成立,假设n=k时命题成立,证明当n=k+1时命题也成立.
(2)由(1)猜想数列{an}的通项公式:an=
| n |
| n-1 |
解答:解:(1)易求得a1=1,a2=
-1,a3=
-
(3分);
(2)猜想an=
-
(n∈N*)(5分)
证明:①当n=1时,a1=
-
=1,命题成立
②假设n=k时,ak=
-
成立,(8分)
则n=k+1时,ak+1=Sk+1-Sk=
(ak+1+
)-
(ak+
)=
(ak+1+
)-
(
-
+
)=
(ak+1+
)-
,
所以,
+2
ak+1-1=0,∴ak+1=
-
.
即n=k+1时,命题成立.
由①②知,n∈N*时,an=
-
.(12分)
| 2 |
| 3 |
| 2 |
(2)猜想an=
| n |
| n-1 |
证明:①当n=1时,a1=
| 1 |
| 0 |
②假设n=k时,ak=
| k |
| k-1 |
则n=k+1时,ak+1=Sk+1-Sk=
| 1 |
| 2 |
| 1 |
| ak+1 |
| 1 |
| 2 |
| 1 |
| ak |
| 1 |
| 2 |
| 1 |
| ak+1 |
| 1 |
| 2 |
| k |
| k-1 |
| 1 | ||||
|
| 1 |
| 2 |
| 1 |
| ak+1 |
| k |
所以,
| a | 2 k+1 |
| k |
| k+1 |
| k |
即n=k+1时,命题成立.
由①②知,n∈N*时,an=
| n |
| n-1 |
点评:本题是中档题,考查数列递推关系式的应用,数学归纳法证明数列问题的方法,考查逻辑推理能力,计算能力.注意在证明n=k+1时用上假设,化为n=k的形式.

练习册系列答案
相关题目
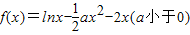
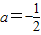 且关于x的方程
且关于x的方程 在[1,4]上恰有两个不相等的实数根,求实数b的取值范围;
在[1,4]上恰有两个不相等的实数根,求实数b的取值范围;