题目内容
已知函数f(x)为二次函数,不等式f(x)+2<0的解集为(-1,
),且对任意的a,β∈R,恒有f(sinα)≤0,f(2+cosβ)≥0.
(1)求f(x)的解析式;
(2)若数列{an}满足a1=1,3an+1=1-
(n∈N*),求数列{an}的通项公式;
(3)设bn=
,在(2)的条件下,若数列{bn}的前n项和为Sn,求数列{Sn•cos(bnπ)}的前n项和Tn.
| 1 |
| 3 |
(1)求f(x)的解析式;
(2)若数列{an}满足a1=1,3an+1=1-
| 1 | ||
f(an+1)-f(an)-
|
(3)设bn=
| 1 |
| an |
分析:(1)由不等式的解集设出f(x)+2的两根式,对角α,β取特值后得到f(1)=1,由此可取函数f(x)的解析式;
(2)求出f(an+1),f(an),代入已知的等式中化简得到数列{
}为等差数列,求出数列{
}的通项公式后可求数列{an}的通项公式;
(3)由bn=
,求出cos(bnπ),然后分n为偶数和奇数讨论求解数列{Sn•cos(bnπ)}的前n项和Tn.
(2)求出f(an+1),f(an),代入已知的等式中化简得到数列{
| 1 |
| an |
| 1 |
| an |
(3)由bn=
| 1 |
| an |
解答:解:(1)设f(x)+2=a(x+1)(x-
)(a>0),即f(x)=ax2+
x-
-2.
取α=
,β=π,代入f(sinα)≤0,f(2+cosβ)≥0,则f(1)≤0,f(1)≥0同时成立,
故f(1)=0,解得a=
,故f(x)=
x2+x-
;
(2)∵f(an+1)-f(an)=
(an+1)2+(an+1)-
-(
an2+an-
)=3an+
.
∴3an+1=1-
=1-
=
.
即
=
+3.故数列{
}为等差数列.
∵
=1,∴
=3n-2,an=
;
(3)∵bn=3n-2,∴cos(bnπ)=cos(3n-2)π=
k∈N*
即Sn•cos(bnπ)=(-1)nSn,∴Tn=-S1+S2-S3+S4-…+(-1)nSn.
①当n为偶数时,Tn=(-S1+S2)+(-S3+S4)+…+(-Sn-1+Sn)
=b2+b4+…+bn=
.
②当n为奇数时,
Tn=Tn-1-Sn=
-
=
.
综上,Tn=
.
| 1 |
| 3 |
| 2a |
| 3 |
| a |
| 3 |
取α=
| π |
| 2 |
故f(1)=0,解得a=
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
(2)∵f(an+1)-f(an)=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
∴3an+1=1-
| 1 | ||
f(an+1)-f(an)-
|
| 1 |
| 3an+1 |
| 3an |
| 3an+1 |
即
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an |
∵
| 1 |
| a1 |
| 1 |
| an |
| 1 |
| 3n-2 |
(3)∵bn=3n-2,∴cos(bnπ)=cos(3n-2)π=
|
即Sn•cos(bnπ)=(-1)nSn,∴Tn=-S1+S2-S3+S4-…+(-1)nSn.
①当n为偶数时,Tn=(-S1+S2)+(-S3+S4)+…+(-Sn-1+Sn)
=b2+b4+…+bn=
| 3n2+2n |
| 4 |
②当n为奇数时,
Tn=Tn-1-Sn=
| 3(n-1)2+2(n-1) |
| 4 |
| n(1+3n-2) |
| 2 |
| -3n2-2n+1 |
| 4 |
综上,Tn=
|
点评:本题考查了一元二次不等式的解法,考查了数列的函数特性,考查了数列的递推式及数列的和,考查了分类讨论的数学思想方法,考查了学生综合处理和解决问题的能力,是有一定难度题目.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
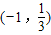 ,且对任意的a,β∈R,恒有f(sinα)≤0,f(2+cosβ)≥0.
,且对任意的a,β∈R,恒有f(sinα)≤0,f(2+cosβ)≥0.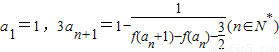 ,求数列{an}的通项公式;
,求数列{an}的通项公式;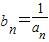 ,在(2)的条件下,若数列{bn}的前n项和为Sn,求数列{Sn•cos(bnπ)}的前n项和Tn.
,在(2)的条件下,若数列{bn}的前n项和为Sn,求数列{Sn•cos(bnπ)}的前n项和Tn.