题目内容
已知y=f(x)为二次函数,若y=f(x)在x=2处取得最小值-4,且y=f(x)的图象经过原点,
(1)求f(x)的表达式;
(2)求函数y=f(log
x)在区间[
,2]上的最大值和最小值.
(1)求f(x)的表达式;
(2)求函数y=f(log
| 1 |
| 2 |
| 1 |
| 8 |
分析:(1)利用待定系数法求二次函数的解析式即可.
(2)根据对数函数的单调性和二次函数的性质进行求值.
(2)根据对数函数的单调性和二次函数的性质进行求值.
解答:解:(1)设二次函数f(x)=a(x-2)2-4,
∵函数图象过原点,
∴f(0)=0,解得a=1,
∴f(x)=(x-2)2-4.
(2)∵x∈[
,2],∴log
x∈[-1,3],设t=log
x,则t∈[-1,3],
则g(t)=(t-2)2-4.且t∈[-1,3],
∴当t=2即x=
时,函数y有最小值-4,
当t=-1,即x=2时,函数y有最大值5.
∵函数图象过原点,
∴f(0)=0,解得a=1,
∴f(x)=(x-2)2-4.
(2)∵x∈[
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
则g(t)=(t-2)2-4.且t∈[-1,3],
∴当t=2即x=
| 1 |
| 4 |
当t=-1,即x=2时,函数y有最大值5.
点评:本题主要考查二次函数的图象和性质以及对数函数的基本运算,利用换元法将条件转化为二次函数是解决本题的关键.

练习册系列答案
相关题目
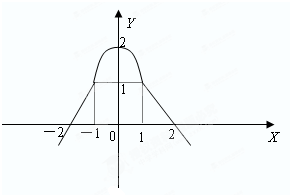 已知y=f(x)的定义域为R,其图象是由两条射线和二次函数图象的一部分构成,其中(0,2)顶点,如图所示
已知y=f(x)的定义域为R,其图象是由两条射线和二次函数图象的一部分构成,其中(0,2)顶点,如图所示