题目内容

设m、n是两条不同的直线，、β是两个不同的平面，则下列命题中正确的是

A．若m∥n，m∥，则n∥

B．若⊥β，m∥，则m⊥β

C．若⊥β，m⊥β，则m∥

D．若m⊥n，m⊥，n⊥β，则⊥β

 

【答案】

D

【解析】

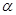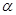试题分析：A．若m∥n，m∥，则n∥ 或者 n ；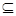

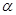B．若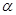⊥β，m∥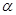，则m与β可能平行，可能相交，也可能在平面内。

C．若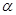⊥β，m⊥β，则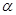m∥或者 m ；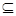     

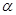D．若m⊥n，m⊥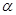，n⊥β，则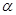⊥β，此命题正确。

考点：线面平行的判定定理；空间中线、面的位置关系。

点评：本小题主要考查空间中线、面的各种位置关系，解题时要灵活运用立体几何中各位置关系的判定定理和性质定理，并借助空间想象寻找反例，判断命题的真假，这种类型的问题在高考选择题中非常普遍．

 

练习册系列答案
相关题目
12、设m，n是两条不同的直线，α，β，γ是三个互不相同的平面，给出下列命题：①若m?β，α⊥β，则m⊥α；②若α∩γ=m，β∩γ=n，α∥β，则m∥n；③若m∥n，m⊥α，n⊥β，则α∥β；④若α⊥γ，β⊥γ，则α∥β，其中正确的命题的序号为
②③
．
8、设m，n是两条不同的直线，α，β，γ是三个不同的平面．有下列四个命题：
①若m?β，α⊥β，则m⊥α；
②若α∥β，m?α，则m∥β；
③若n⊥α，n⊥β，m⊥α，则m⊥β；
④若α⊥γ，β⊥γ，m⊥α，则m⊥β．
其中正确命题的序号是（　　）
5、4．设m、n是两条不同的直线，α、β是两相没的平面，则下列命题中的真命题是（　　）
（2012•贵溪市模拟）设m、n是两条不同的直线α，β，γ，是三个不同的平面，下列四个命题中正确的序号是（　　）
①若m⊥α，n∥α，则m⊥n     
②若α⊥γ，β⊥γ，则α∥β   
③若m∥α，n∥α，则m∥n    
④若α∥β，β∥γ，m⊥α，则m⊥γ
设m，n是两条不同的直线，α，β是两个不同的平面．考查下列命题，其中不正确的命题有
①③④
①③④
．（填上所有符合条件命题的序号）
①m⊥α，n?β，m⊥n⇒α⊥β；      ②α∥β，m⊥α，n∥β⇒m⊥n；
③α⊥β，m⊥α，n∥β⇒m⊥n；       ④α⊥β，α∩β=m，n⊥m⇒n⊥β．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网