题目内容
(本题满分12分).以下是粤西地区某县搜集到的新房屋的销售价格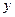 和
和 房屋的面积
房屋的面积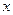 的数据:
的数据: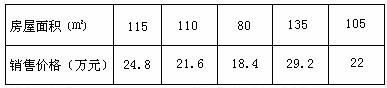
(1)画出数据散点图;
(2)由散点图判断新房屋销售价格y和房屋面积x是否具有线性相关关系?若有,求线性回 归方程。(保留四位小数)
归方程。(保留四位小数)
(3)根据房屋面积预报销售价格的回归方程,预报房屋面积为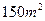 时的销售价格。
时的销售价格。
参考公式: 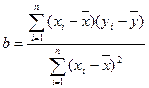 ,
,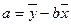
参考数据: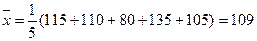 ,
,
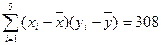 ,
,
(12分).解1
 )数据对应的散点图如图所示:3分
)数据对应的散点图如图所示:3分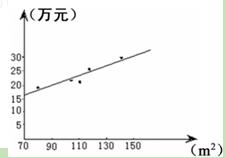
(2)从散点图可以看出,样本点呈条状分布,房屋销售面积与销售价格有比较好的线性相关关系, 4分
设所求回归直线方程为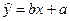 ,
,
则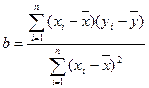 =
=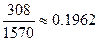 , 6分
, 6分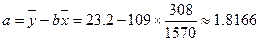 ,……………………8分
,……………………8分
故所求回归直线方程为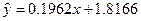 .………………………………10分
.………………………………10分
(3)当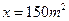 时,销售价格的估计值为:
时,销售价格的估计值为: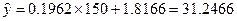 (万元).…………………………12分
(万元).…………………………12分
解析

 初中学业考试导与练系列答案
初中学业考试导与练系列答案(本题满分13分)某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中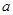 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比
如下表所示,求数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
(本小题满分12分)
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组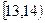 ,第二组
,第二组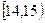 ……第五组
……第五组 ,如图是按上述分组方法
,如图是按上述分组方法 得到的频率分布直方图.
得到的频率分布直方图.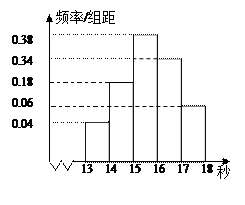
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
( II )根据有关规定,成绩小于16秒为达标.
(ⅰ)用样本估计总体,某班有学生45人,设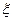 为达标人数,求
为达标人数,求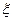 的数学期望与方差.
的数学期望与方差.
(ⅱ)如果男女生使用相同的达标标准,则男女
生达标情况如下表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 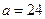 | 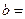 ______ ______ | _____ |
| 不达标 |  _____ _____ |  | _____ |
| 合计 | ______ | ______ |  |
根据上表数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2) 试预测加工10个零件需要多少时间?

(本小题满分12分)
对某电子元件进行寿命追踪调查,情况如下:
| 寿命/小时 | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
| 分组 | 频数 | 频率 |
| 100~200 | | |
| 200~300 | | |
| 300~400 | | |
| 400~500 | | |
| 500~600 | | |
| 合计 | | |
(3)估计电子元件寿命在100~400小时以内的频率;
(本小题满分12分)品厂为了检查甲、乙两条自动包装流水线的生产情况,在这两条
流水线上各抽取40件产品作为样本称 出它们的重量(单位:克),重量值落在(495,510]
出它们的重量(单位:克),重量值落在(495,510]
的产 品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,
品为合格品,否则为不合格品,表1是甲流水线样本频数分布表, 图1是乙流水线样
图1是乙流水线样
本的频率分布直方图。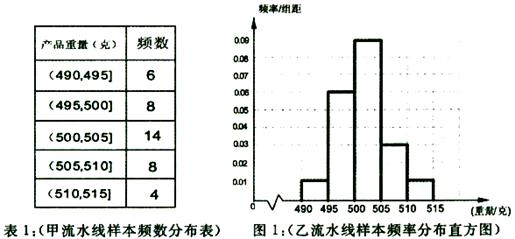 某食
某食
(1)若检验员不小心将甲、乙两条流水线生产的重量值在(510,515]的产品放在了一起,
然后又随机取出3件产品,求至少有一件是乙流水线生产的产品的概率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
| | 甲流水线 | 乙流水线 | 合 计 |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | | | n= |

 学共有学生2000名,各年级男、女生人数如下表:
学共有学生2000名,各年级男、女生人数如下表:


 ,
, ,求高三年级
,求高三年级 中女生比男生多的概率.
中女生比男生多的概率.