题目内容
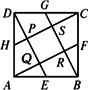
如图，在边长为2的正方形ABCD中，E、F、G、H分别是各自所在边的中点，连结AF、BG、CH、DE，得到一个小正方形PQRS，求小正方形PQRS的面积．
答案：
解析：
提示：
解析：
|
易知正方形ABCD的中心M(1，1)，就是正方形PQRS的中心，而E(1，0)、D(0，2)，直线ED的方程为l：2x＋y－2＝0． M到直线l的距离为 |
，小正方形的边长为
，面积为
．提示：
|
利用对称性求解，求出大正方形的中心后，利用点到直线的距离公式求出中心到一边的距离，即为小正方形边长的一半，从而可求出小正方形的面积． |
练习册系列答案
天天练口算系列答案
相关题目
（2013•资阳模拟）如图，在边长为2的正六边形ABCDEF中，P是△CDE内（含边界）的动点，设向量
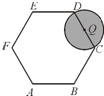如图，在边长为2的正六边形ABCDEF中，动圆Q的半径为1，圆心在线段CD（含端点）上运动，P是圆Q上及内部的动点，设向量| AP |
| AB |
| AF |
| A、（1，2] |
| B、[5，6] |
| C、[2，5] |
| D、[3，5] |
的起点、终点和模;
共线的向量;
相等的向量.