题目内容
已知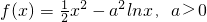 .
.
(I)求函数f(x)的最小值;
( II)(i)设0<t<a,证明:f(a+t)<f(a-t).
(ii)若f(x1)=f(x2),且x1≠x2.证明:x1+x2>2a.
(Ⅰ)解:函数的定义域为(0,+∞).求导数,可得f′(x)=x-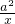 =
=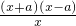 .…(1分)
.…(1分)
当x∈(0,a)时,f′(x)<0,f(x)单调递减;当x∈(a,+∞)时,f′(x)>0,f(x)单调递增.
当x=a时,f(x)取得极小值也是最小值f(a)= a2-a2lna.…(4分)
a2-a2lna.…(4分)
(Ⅱ)证明:(ⅰ)设g(t)=f(a+t)-f(a-t),则
当0<t<a时,g′(t)=f′(a+t)+f′(a-t)=a+t-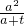 +a-t-
+a-t-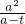 =
=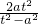 <0,…(6分)
<0,…(6分)
所以g(t)在(0,a)单调递减,g(t)<g(0)=0,即f(a+t)-f(a-t)<0,
故f(a+t)<f(a-t).…(8分)
(ⅱ)由(Ⅰ),f(x)在(0,a)单调递减,在(a,+∞)单调递增,
不失一般性,设0<x1<a<x2,
因0<a-x1<a,则由(ⅰ),得f(2a-x1)=f(a+(a-x1))<f(a-(a-x1))=f(x1)=f(x2),…(11分)
又2a-x1,x2∈(a,+∞),
故2a-x1<x2,即x1+x2>2a.…(12分)
分析:(Ⅰ)确定函数的定义域,并求导函数,确定函数的单调性,可得x=a时,f(x)取得极小值也是最小值;
(Ⅱ)(ⅰ)构造函数g(t)=f(a+t)-f(a-t),当0<t<a时,求导函数,可知g(t)在(0,a)单调递减,所以g(t)<g(0)=0,即可证得;
(ⅱ)由(Ⅰ),f(x)在(0,a)单调递减,在(a,+∞)单调递增,不失一般性,设0<x1<a<x2,所以0<a-x1<a,利用(ⅰ)即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性、极值、最值,考查不等式的证明,解题的关键是构造函数,确定函数的单调性.
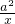 =
=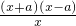 .…(1分)
.…(1分)当x∈(0,a)时,f′(x)<0,f(x)单调递减;当x∈(a,+∞)时,f′(x)>0,f(x)单调递增.
当x=a时,f(x)取得极小值也是最小值f(a)=
 a2-a2lna.…(4分)
a2-a2lna.…(4分)(Ⅱ)证明:(ⅰ)设g(t)=f(a+t)-f(a-t),则
当0<t<a时,g′(t)=f′(a+t)+f′(a-t)=a+t-
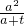 +a-t-
+a-t-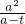 =
=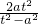 <0,…(6分)
<0,…(6分)所以g(t)在(0,a)单调递减,g(t)<g(0)=0,即f(a+t)-f(a-t)<0,
故f(a+t)<f(a-t).…(8分)
(ⅱ)由(Ⅰ),f(x)在(0,a)单调递减,在(a,+∞)单调递增,
不失一般性,设0<x1<a<x2,
因0<a-x1<a,则由(ⅰ),得f(2a-x1)=f(a+(a-x1))<f(a-(a-x1))=f(x1)=f(x2),…(11分)
又2a-x1,x2∈(a,+∞),
故2a-x1<x2,即x1+x2>2a.…(12分)
分析:(Ⅰ)确定函数的定义域,并求导函数,确定函数的单调性,可得x=a时,f(x)取得极小值也是最小值;
(Ⅱ)(ⅰ)构造函数g(t)=f(a+t)-f(a-t),当0<t<a时,求导函数,可知g(t)在(0,a)单调递减,所以g(t)<g(0)=0,即可证得;
(ⅱ)由(Ⅰ),f(x)在(0,a)单调递减,在(a,+∞)单调递增,不失一般性,设0<x1<a<x2,所以0<a-x1<a,利用(ⅰ)即可证得结论.
点评:本题考查导数知识的运用,考查函数的单调性、极值、最值,考查不等式的证明,解题的关键是构造函数,确定函数的单调性.

练习册系列答案
相关题目
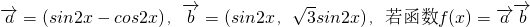 .
.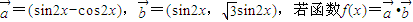 .
.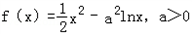 .
. .
. .
.