题目内容
已知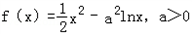 .
.
(I)求函数f(x)的最小值;
( II)当x>2a,证明: .
.
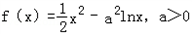 .
.(I)求函数f(x)的最小值;
( II)当x>2a,证明:
 .
.解:(Ⅰ)f′(x)=x﹣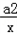 =
= 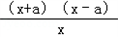 .
.
当x∈(0,a)时,f′(x)<0,f(x)单调递减;
当x∈(a,+∞)时,f′(x)>0,f(x)单调递增.
当x=a时,f(x)取得极小值也是最小值f(a)= a2﹣a2lna.
a2﹣a2lna.
(Ⅱ)由(Ⅰ),f(x)在(2a,+∞)单调递增,
则所证不等式等价于f(x)﹣f(2a)﹣ a(x﹣2a)>0.
a(x﹣2a)>0.
设g(x)=f(x)﹣f(2a)﹣ a(x﹣2a),
a(x﹣2a),
则当x>2a时, g′(x)=f′(x)﹣ a=x﹣
a=x﹣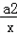 ﹣
﹣ a=
a= 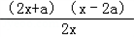 >0,
>0,
所以g(x)在[2a,+∞)上单调递增,
当x>2a时,g(x)>g(2a)=0,即f(x)﹣f(2a)﹣ a(x﹣2a)>0,
a(x﹣2a)>0,
故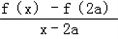 >
> a.
a.
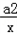 =
= 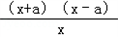 .
.当x∈(0,a)时,f′(x)<0,f(x)单调递减;
当x∈(a,+∞)时,f′(x)>0,f(x)单调递增.
当x=a时,f(x)取得极小值也是最小值f(a)=
 a2﹣a2lna.
a2﹣a2lna.(Ⅱ)由(Ⅰ),f(x)在(2a,+∞)单调递增,
则所证不等式等价于f(x)﹣f(2a)﹣
 a(x﹣2a)>0.
a(x﹣2a)>0.设g(x)=f(x)﹣f(2a)﹣
 a(x﹣2a),
a(x﹣2a),则当x>2a时, g′(x)=f′(x)﹣
 a=x﹣
a=x﹣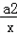 ﹣
﹣ a=
a= 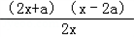 >0,
>0,所以g(x)在[2a,+∞)上单调递增,
当x>2a时,g(x)>g(2a)=0,即f(x)﹣f(2a)﹣
 a(x﹣2a)>0,
a(x﹣2a)>0,故
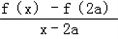 >
> a.
a.
练习册系列答案
相关题目
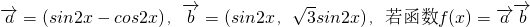 .
.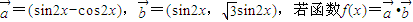 .
.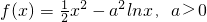 .
. .
.