题目内容
在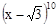 的展开式中,
的展开式中,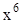 的系数为( )
的系数为( )
A.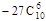 | B.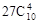 | C.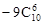 | D.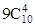 |
D
解析试题分析: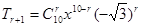 ,令
,令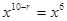 ,即
,即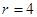 ,所以
,所以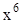 的系数为
的系数为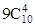 .
.
考点:二项式系数
点评:此题主要考查二项式系数的性质问题,其中涉及到展开式中通项公式的求法问题,对于此类考点在高
考中多以选择填空的形式出现,考查内容较简单,同学们需要掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知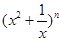 的展开式的二项式系数之和为32,则展开式中含
的展开式的二项式系数之和为32,则展开式中含 项的系数是( )
项的系数是( )
| A.5 | B.20 | C.10 | D.40 |
男女生共8人,从中任选3人,出现2个男生,1个女生的概率为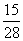 ,则其中女生人数是
,则其中女生人数是
| A.2人 | B.3人 | C.4人 | D.2人或3人 |
高二某同学有A、B两类不同的校庆明信片,其中A类明信片2张,B类明信片3张,他想从中取出4张寄给初中的4位老师,每位老师1张,则不同的选择方法有( )
| A.4种 | B.10种 | C.18种 | D.20种 |
某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数有( )
| A.6种 | B.24种 | C.180种 | D.90种 |
设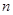 为奇数,那么
为奇数,那么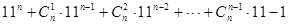 除以13的余数是( )
除以13的余数是( )
A.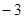 | B.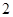 | C.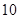  | D.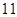 |
从0,1,2,3,4,5六个数中任取四个互异的数字组成四位数,个位,百位上必排偶数数字的四位数共有( )
| A.52个 | B.60个 | C.54 | D.66个 |
某公共汽车上有10名乘客,沿途有5个车站,乘客下车的可能方式有( )
A.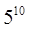 种 种 | B.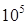 种 种 | C.50种 | D.10种 |
若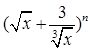 展开式中存在常数项,则n的最小值为( )
展开式中存在常数项,则n的最小值为( )
| A.5 | B.6 | C.7 | D.8 |