题目内容
已知函数 的导函数为
的导函数为  ,满足
,满足  ,且
,且 ,则
,则 的单调性情况为
的单调性情况为
A.先增后减 B单调递增 C.单调递减 D先减后增
C
解析试题分析:由 知,
知,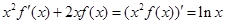 ,故
,故 =
=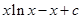 ,所以
,所以 =
=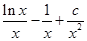 ,因为
,因为 ,所以c=
,所以c=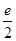 ,所以
,所以 =
=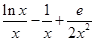 ,所以
,所以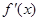 =
= =
=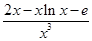 ,设
,设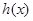 =
=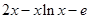 ,所以
,所以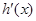 =
=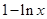 ,
,
当0< <
< 时,
时,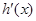 >0,当
>0,当 >
> 时,
时,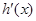 <0,则
<0,则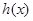 在(0,
在(0, )是增函数,在(
)是增函数,在( ,+
,+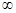 )上是减函数,所以当
)上是减函数,所以当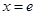 时,
时,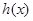 取最大值
取最大值 =0,所以当
=0,所以当 >0时,
>0时,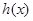 ≤0,即
≤0,即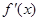 ≤0,所以
≤0,所以 单调递减,故选C.
单调递减,故选C.
考点:常见函数的导数,导数的运算法则,导数的综合运用

练习册系列答案
相关题目
曲线f(x)=x3+x﹣2在p0处的切线平行于直线y=4x﹣1,则p0的坐标为( )
| A.(1,0) | B.(2,8) |
| C.(1,0)或(﹣1,﹣4) | D.(2,8)或(﹣1,﹣4) |
已知函数 对任意的
对任意的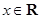 满足
满足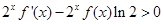 (其中
(其中 是函数
是函数 的导函数),则下列不等式成立的是( )
的导函数),则下列不等式成立的是( )
A.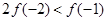 | B.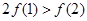 |
C.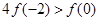 | D.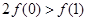 |
由直线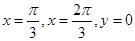 与曲线
与曲线 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
| A.1 | B. | C. | D.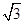 |
若函数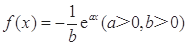 的图象在
的图象在 处的切线与圆
处的切线与圆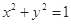 相切,则
相切,则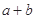 的最大值是( )
的最大值是( )
| A.4 | B.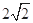 | C.2 | D.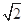 |
若 ,则
,则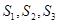 的大小关系为( )
的大小关系为( )
A. | B.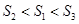 | C.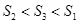 | D.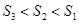 |
 的图像经过坐
的图像经过坐 标原
标原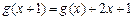 ,设函数
,设函数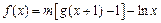 ,其中m为常数且
,其中m为常数且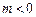 。
。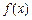 的单调性并说明理由。
的单调性并说明理由。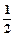 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说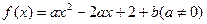 ,在区间
,在区间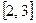 上有最大值5,最小
上有最大值5,最小 上单调,求
上单调,求 的取值范围。
的取值范围。