题目内容
12.在等差数列{an}中,a16+a17+a18=a9=-18,其前n项和为Sn.(1)求Sn的最小值;
(2)求出Sn取最小值时n的值.
分析 (1)由已知数据可得等差数列{an}的公差d,进而可得a1,可得Sn,由二次函数可得;
(2)由(1)的求解过程可得.
解答 解:(1)∵在等差数列{an}中a16+a17+a18=a9=-18,
∴a16+a17+a18=3a17=-18,∴a17=-6,
∴公差d=$\frac{{a}_{17}-{a}_{9}}{17-9}$=$\frac{-6-(-18)}{8}$=$\frac{3}{2}$,
∴a9=a1+8d=a1+8×$\frac{3}{2}$=-18,解得a1=-30,
∴Sn=-30n+$\frac{n(n-1)}{2}$×$\frac{3}{2}$=$\frac{1}{4}$(3n2-123n),
由二次函数可知当n=$-\frac{-123}{2×3}$=20$\frac{1}{2}$时取最小值,
结合n为正整数和二次函数的对称性可知当n=20或21时,Sn取最小值,
代值计算可得S21=S20=$\frac{1}{4}$(3×202-123×20)=-315;
(2)由(1)知当Sn取最小值时n的值为20或21.
点评 本题考查等差数列的求和公式和二次函数的最值,属中档题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
2.若$\overrightarrow{z}$是z的共轭复数,且满足$\overrightarrow{z}$•(1-i)2=4+2i,则z=( )
| A. | -1+2i | B. | -1-2i | C. | 1+2i | D. | 1-2i |
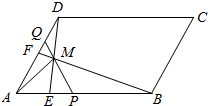 如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.
如图所示,在平行四边形ABCD中,$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{2}$$\overrightarrow{AD}$,BF与DE交于点M,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$.