题目内容
若命题p:?∈R,
>0,则其否定是
| 1 |
| x2+x+1 |
存在x0∈R使
≤0
| 1 |
| x02+x0+1 |
存在x0∈R使
≤0
.| 1 |
| x02+x0+1 |
分析:根据全称命题和特称命题、命题的否定的定义,求出命题p:?∈R,
>0的否定.
| 1 |
| x2+x+1 |
解答:解:根据“命题的否定”的定义,若命题p:?∈R,
>0,
则它的否定为:存在x0∈R使
≤0,或x02+x0+1=0,
故答案为 存在x0∈R使
≤0.
| 1 |
| x2+x+1 |
则它的否定为:存在x0∈R使
| 1 |
| x02+x0+1 |
故答案为 存在x0∈R使
| 1 |
| x02+x0+1 |
点评:本题主要考查全称命题和特称命题的定义,求命题的否定,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
若命题p:?α∈R,cos(π-α)=cosα;命题q:?x∈R,x2+1>0.则下面结论正确的是( )
| A、p是假命题 | B、¬q是真命题 | C、p∧q是假命题 | D、p∨q是真命题 |
已知命题P: 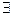 x∈R,mx2+1≤0,命题q:
x∈R,mx2+1≤0,命题q: 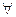 x∈R,x2+mx+1>0 ,若p∨q 为假命题,则实数m的取值范围为 ( )
x∈R,x2+mx+1>0 ,若p∨q 为假命题,则实数m的取值范围为 ( )
| A.m≤-2 | B.m≥2 |
| C.m≤-2或m≥2 | D.-2≤ m≤ 2 m≤ 2 |
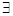 x∈R,mx2+1≤0,命题q:
x∈R,mx2+1≤0,命题q: 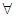 x∈R,x2+mx+1>0 ,若p∨q 为假命题,则实数m的取值范围为 ( )
x∈R,x2+mx+1>0 ,若p∨q 为假命题,则实数m的取值范围为 ( )