题目内容
设数列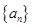 的前
的前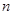 项和为
项和为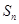 ,且
,且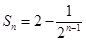 .
.
(1)求数列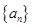 的通项公式;
的通项公式;
(2)设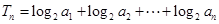 ,求证:
,求证: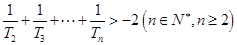 .
.
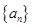 的前
的前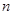 项和为
项和为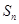 ,且
,且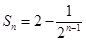 .
.(1)求数列
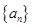 的通项公式;
的通项公式;(2)设
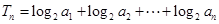 ,求证:
,求证: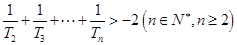 .
.(1)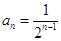 ;(2)详见解析.
;(2)详见解析.
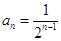 ;(2)详见解析.
;(2)详见解析.试题分析:(1)在
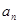 和
和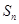 的关系式中,先利用
的关系式中,先利用 这一特点,令
这一特点,令 代入式子中求出
代入式子中求出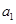 的值,然后令
的值,然后令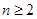 ,由
,由 求出
求出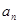 的表达式,然后就
的表达式,然后就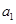 的值是否符合
的值是否符合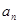 的通项进行检验,从而最终确定数列
的通项进行检验,从而最终确定数列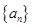 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列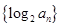 的通项公式,根据通项公式的特点利用等差数列求和公式求出
的通项公式,根据通项公式的特点利用等差数列求和公式求出 ,然后根据数列
,然后根据数列 的通项公式的特点选择裂项法求和
的通项公式的特点选择裂项法求和 ,从而证明相应不等式.
,从而证明相应不等式.试题解析:(1)当
 时,
时, .
.当
 时,
时, ,此式对
,此式对 也成立.
也成立.
 .
.(2)证明:设
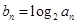 ,则
,则 .
. 所以
 是首项为
是首项为 ,公差为
,公差为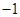 的等差数列.
的等差数列.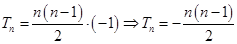 ,
,
 .
.
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
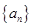 的前
的前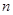 项和为
项和为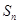 ,且
,且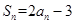
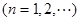 .
.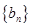 满足
满足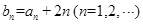 ,求数列
,求数列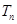 .
.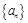 中,
中,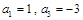 .
.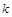 项和
项和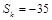 ,求
,求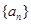 的集合:①对任意
的集合:①对任意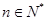 ,
,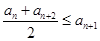 恒成立;②对任意
恒成立;②对任意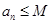 恒成立.
恒成立.
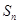 是其前n项和,且
是其前n项和,且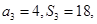 试探究数列
试探究数列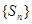 与集合W之间的关系;
与集合W之间的关系;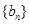 的通项公式为
的通项公式为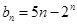 ,且
,且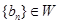 ,求M的取值范围.
,求M的取值范围. 满足:
满足: ,
, 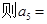 ( )
( )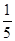

 的前n项和是
的前n项和是 ,若
,若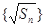 都是等差数列,且公差相等,则
都是等差数列,且公差相等,则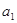 =_______________.
=_______________.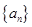 的首项
的首项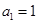 ,公比
,公比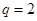 ,则
,则 ( )
( )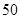


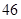
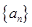 的公差不为零,首项
的公差不为零,首项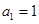 ,
,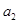 是
是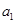 和
和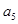 的等比中项,则数列的前
的等比中项,则数列的前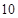 项之和是 ( )
项之和是 ( )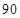
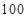
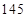
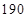
 的前项和为
的前项和为 ,若
,若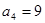 ,
,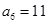 ,则
,则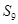 等于( )
等于( )