题目内容
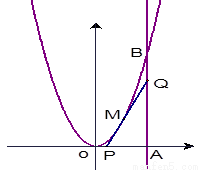
(本题满分10分) 如图,由y=0,x=8,y=x2围成的曲边三角形,在曲线弧OB上求一点M,使得过M所作的y=x2的切线PQ与OA,AB围成的三角形PQA面积最大。
【答案】
(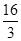 ,
,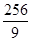 )
)
【解析】
试题分析:如图,设点M(t,t2),容易求出过点M的切线的斜率为2t,即切线方程为y-t2=2t(x-t),(0≤t≤8)
当t=0时,切线为y=0,△PQA不存在,所以(0<t≤8).
在切线方程中令y=0,得到P点的横坐标为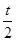 ,令x=8,得到Q点的纵坐标为16t-t2
,令x=8,得到Q点的纵坐标为16t-t2
所以S△PQA= 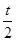 (8-
(8-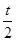 )(16t-t2),
)(16t-t2),
令S′(t)=(8-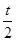 )(8-
)(8-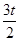 )=0;
)=0;
解可得得t=16(舍去)或t=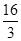 ;
;
由二次函数的性质分析易得,
t=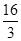 是S△PQA=
是S△PQA=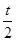 (8-
(8-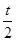 )(16t-t2)的极大值点;
)(16t-t2)的极大值点;
从而当t=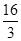 时,面积S(t)有最大值Smax=S(
时,面积S(t)有最大值Smax=S(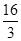 )=
)=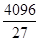 ,此时M(
,此时M(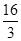 ,
,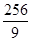 )
)
考点:本题主要考查导数的几何意义的应用,应用导数求函数的最值问题。
点评:本题符合高考考试大纲,是一道颇具代表性的题目。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,求证:
,求证: ;
; ,求证:三数
,求证:三数 ,
, ,
, 中至少有一个不小于2.
中至少有一个不小于2.
 的所有棱长都为2,
的所有棱长都为2, 为棱
为棱 的中点,
的中点, 平面
平面 ;
; 的余弦值大小.
的余弦值大小.
 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
, ,
, ,求两景点
,求两景点