题目内容
已知函数 在区间上[1,3]的函数值大于0恒成立,则实数a的取值范围是( )
在区间上[1,3]的函数值大于0恒成立,则实数a的取值范围是( )A.

B.

C.(1,+∞)
D.

【答案】分析:设g(x)=(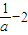 )x+1,x∈[1,3]可得g(x)=(
)x+1,x∈[1,3]可得g(x)=( )x+1是定义域上的单调函数,即
)x+1是定义域上的单调函数,即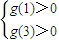 解得:0<a<
解得:0<a<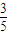 .所以
.所以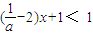 在区间上[1,3]恒成立,
在区间上[1,3]恒成立,
所以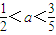 .
.
解答:解:设g(x)=(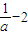 )x+1,x∈[1,3]
)x+1,x∈[1,3]
所以g(x)=(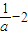 )x+1是定义域上的单调函数,
)x+1是定义域上的单调函数,
根据题意得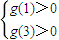 解得:0<a<
解得:0<a<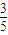
因为函数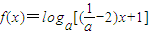 在区间上[1,3]的函数值大于0恒成立
在区间上[1,3]的函数值大于0恒成立
所以 在区间上[1,3]恒成立
在区间上[1,3]恒成立
所以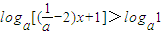 在区间上[1,3]恒成立
在区间上[1,3]恒成立
因为0<a<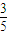
所以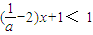 在区间上[1,3]恒成立
在区间上[1,3]恒成立
即 在区间上[1,3]恒成立
在区间上[1,3]恒成立
所以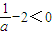
解得a>
所以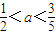
所以实数a的取值范围是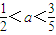 .
.
故选B.
点评:本题主要考查不等式的恒成立问题,解决此题的关键是准确的利用不等式的性质转化不等式,利用充分条件得出最后的结果.
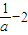 )x+1,x∈[1,3]可得g(x)=(
)x+1,x∈[1,3]可得g(x)=( )x+1是定义域上的单调函数,即
)x+1是定义域上的单调函数,即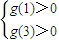 解得:0<a<
解得:0<a<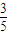 .所以
.所以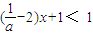 在区间上[1,3]恒成立,
在区间上[1,3]恒成立,所以
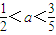 .
.解答:解:设g(x)=(
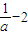 )x+1,x∈[1,3]
)x+1,x∈[1,3]所以g(x)=(
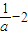 )x+1是定义域上的单调函数,
)x+1是定义域上的单调函数,根据题意得
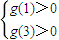 解得:0<a<
解得:0<a<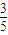
因为函数
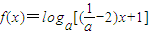 在区间上[1,3]的函数值大于0恒成立
在区间上[1,3]的函数值大于0恒成立所以
 在区间上[1,3]恒成立
在区间上[1,3]恒成立所以
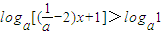 在区间上[1,3]恒成立
在区间上[1,3]恒成立因为0<a<
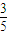
所以
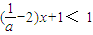 在区间上[1,3]恒成立
在区间上[1,3]恒成立即
 在区间上[1,3]恒成立
在区间上[1,3]恒成立所以
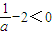
解得a>

所以
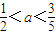
所以实数a的取值范围是
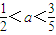 .
.故选B.
点评:本题主要考查不等式的恒成立问题,解决此题的关键是准确的利用不等式的性质转化不等式,利用充分条件得出最后的结果.

练习册系列答案
相关题目
 在区间上[1,3]的函数值大于0恒成立,则实数a的取值范围是( )
在区间上[1,3]的函数值大于0恒成立,则实数a的取值范围是( )


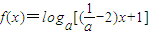 在区间上[1,3]的函数值大于0恒成立,则实数a的取值范围是( )
在区间上[1,3]的函数值大于0恒成立,则实数a的取值范围是( )

