题目内容
若射线OM、ON上分别存在点M1、M2与N1、N2,则三角形面积之比为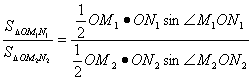 ·
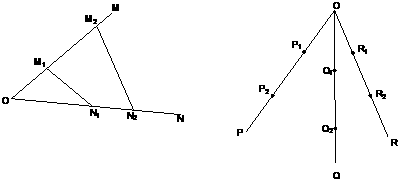
·若不在同一平面内的射线OP、OQ和OR上,分别存在点P1、P2,点Q1、Q2,点R1、R2,则类似的结论是什么?
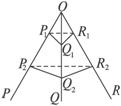
分析:本题已知三角形的面积之比需弄清楚点分得到的结论,然后才能类比得结论扩展到空间的问题.
解:∵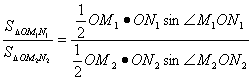 =
=![]() ,
,

其面积比中有一个共同的角,类似地,连结P1Q1、Q1R1、P1R1、P2Q2、Q2R2、P2R2,得到的是锥体,需研究锥体的体积并找出不变量,两条相交线确定一个面,另一条线不在这个面内就有线面角,而线面角不随点的位置变化而变化,设OP与面QRO所成的角为θ.OP在面ORQ内的射影为OP′,P1、P2的射影分别为P1′、P2′,则![]() =sinθ,且
=sinθ,且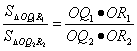 .
.
∴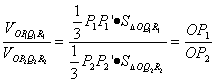 ·
·![]() .
.
∴类似地有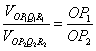 ·
·![]() .
.
绿色通道
要准确地得到相似的结论,需先弄清楚前面的结论是怎么得到的,才能类似地推出.一般地平面内的面积问题推广到空间内为体积问题,平面内的线段问题,推广到空间为面积问题.

练习册系列答案
相关题目
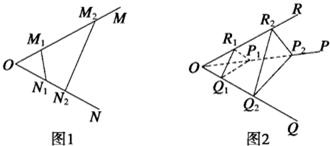
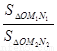 =
=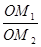 ·
·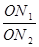 ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是
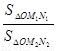 =
=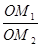 ·
·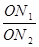 ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是
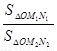 =
=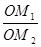 ·
· ;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是
;如图2,若不在同一平面内的射线OP,OQ和OR上分别存在点P1,P2,点Q1,Q2和点R1,R2,则类似的结论是