题目内容
如图1，若射线OM，ON上分别存在点M1，M2与点N1，N2，则| S△OM1N1 |
| S△OM2N2 |
| OM1 |
| OM2 |
| ON1 |
| ON2 |
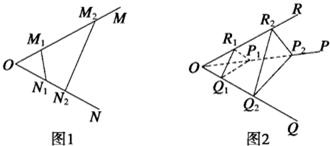
分析：本题考查的知识点是类比推理，在由平面图形的性质向空间物体的性质进行类比时，常用的思路有：由平面图形中点的性质类比推理出空间里的线的性质，由平面图形中线的性质类比推理出空间中面的性质，由平面图形中面的性质类比推理出空间中体的性质．由平面中，若从点O所作的两条射线OM，ON上分别有点M1，M2与点N1，N2，则三角形面积之比为：
=
•
•
（面的性质）我们可以类比在空间中相似的体的性质．
| VO-P1Q1R1 |
| VO-P2Q2R2 |
| OP1 |
| OP2 |
| OQ1 |
| OQ2 |
| OR1 |
| OR2 |
解答：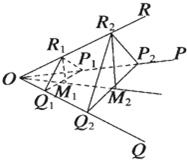
解：类似的结论为：
=
•
•
．（3分）
这个结论是正确的，证明如下：
如图，过R2作R2M2⊥平面P2OQ2于M2，连OM2．过R1在平面OR2M2作R1M1∥R2M2交OM2于M1，
则R1M1⊥平面P2OQ2．由VO-P1Q1R1=
S△P1OQ1•R1M1=
•
OP1•OQ1•sin∠P1OQ1•R1M1
=
OP1•OQ1•R1M1•sin∠P1OQ1，（6分）
同理，VO-P2Q2R2=
OP2•OQ2•R2M2•sin∠P2OQ2．（8分）
∴
=
．（10分）
由平面几何知识可得
=
．
∴
=
．
∴结论正确．（14分）
解：类似的结论为：| VO-P1Q1R1 |
| VO-P2Q2R2 |
| OP1 |
| OP2 |
| OQ1 |
| OQ2 |
| OR1 |
| OR2 |
这个结论是正确的，证明如下：
如图，过R2作R2M2⊥平面P2OQ2于M2，连OM2．过R1在平面OR2M2作R1M1∥R2M2交OM2于M1，
则R1M1⊥平面P2OQ2．由VO-P1Q1R1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 6 |
同理，VO-P2Q2R2=
| 1 |
| 6 |
∴
| VO-P1Q1R1 |
| VO-P2Q2R2 |
| OP1•OQ1•R1M1 |
| OP2•OQ2•R2M2 |
由平面几何知识可得
| R1M1 |
| R2M2 |
| OR1 |
| OR2 |
∴
| VO-P1Q1R1 |
| VO-P2Q2R2 |
| OP1•OQ1•OR1 |
| OP2•OQ2•OR2 |
∴结论正确．（14分）
点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
=
·
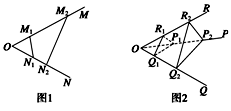
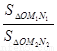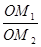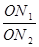；如图2，若不在同一平面内的射线OP，OQ和OR上分别存在点P1，P2，点Q1，Q2和点R1，R2，则类似的结论是什么？这个结论正确吗？说明理由.
=
·
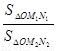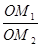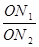；如图2，若不在同一平面内的射线OP，OQ和OR上分别存在点P1，P2，点Q1，Q2和点R1，R2，则类似的结论是
=
·
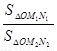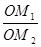；如图2，若不在同一平面内的射线OP，OQ和OR上分别存在点P1，P2，点Q1，Q2和点R1，R2，则类似的结论是
=
·
；如图2，若不在同一平面内的射线OP，OQ和OR上分别存在点P1，P2，点Q1，Q2和点R1，R2，则类似的结论是