题目内容
已知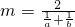 ,
,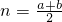
(1)分别就 判断m与n的大小关系,并由此猜想对于任意的a,b∈R+,m与n的大小关系及取得等号的条件;
判断m与n的大小关系,并由此猜想对于任意的a,b∈R+,m与n的大小关系及取得等号的条件;
(2)类比第(1)小题的猜想,得出关于任意的a,b,c∈R+相应的猜想,并证明这个猜想.
解:(1)当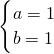 时,m=n=1,当
时,m=n=1,当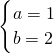 时,
时,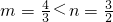 ,…(2分)
,…(2分)
故由此可以猜想:
任意的a,b∈R+,有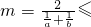
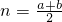 ,当且仅当a=b时取得等号;…(4分)
,当且仅当a=b时取得等号;…(4分)
(2)类比第(1)小题,对于任意的a,b,c∈R+,
猜想: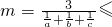
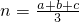 ,当且仅当a=b=c时取得等号.…(5分)
,当且仅当a=b=c时取得等号.…(5分)
证明如下:
对于a,b,c∈R+,要证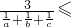
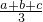 成立,
成立,
只需证: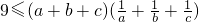 …(7分)
…(7分)
即证: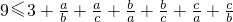
即证: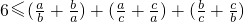 (*) …(9分)
(*) …(9分)
∵对于a,b,c∈R+,有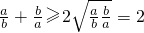
同理: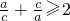 ,
,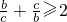 …(11分)
…(11分)
∴不等式(*)成立.
要使(*)的等号成立,必须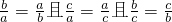 ,
,
故当a=b=c时等号成立. …(12分)
说明:采用其它方法作答的,只是逻辑严密,言之有理,可以根据作答情况酌情给分.
分析:(1)当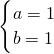 ,
,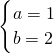 时,分别代入计算,从而可以猜想:任意的a,b∈R+,有
时,分别代入计算,从而可以猜想:任意的a,b∈R+,有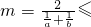
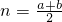 ,当且仅当a=b时取得等号;
,当且仅当a=b时取得等号;
(2)类比第(1)小题,对于任意的a,b,c∈R+,猜想: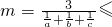
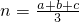 ,当且仅当a=b=c时取得等号利用分析法可以进行证明.
,当且仅当a=b=c时取得等号利用分析法可以进行证明.
点评:本题以大小比较为载体,考查基本不等式的运用,考查类比思想,解题的关键是正确运用基本不等式证明不等式.
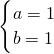 时,m=n=1,当
时,m=n=1,当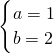 时,
时,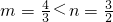 ,…(2分)
,…(2分)故由此可以猜想:
任意的a,b∈R+,有
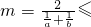
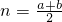 ,当且仅当a=b时取得等号;…(4分)
,当且仅当a=b时取得等号;…(4分)(2)类比第(1)小题,对于任意的a,b,c∈R+,
猜想:
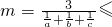
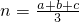 ,当且仅当a=b=c时取得等号.…(5分)
,当且仅当a=b=c时取得等号.…(5分)证明如下:
对于a,b,c∈R+,要证
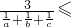
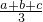 成立,
成立,只需证:
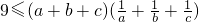 …(7分)
…(7分)即证:
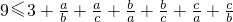
即证:
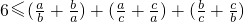 (*) …(9分)
(*) …(9分)∵对于a,b,c∈R+,有
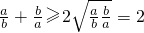
同理:
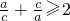 ,
,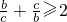 …(11分)
…(11分)∴不等式(*)成立.
要使(*)的等号成立,必须
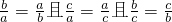 ,
,故当a=b=c时等号成立. …(12分)
说明:采用其它方法作答的,只是逻辑严密,言之有理,可以根据作答情况酌情给分.
分析:(1)当
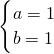 ,
,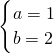 时,分别代入计算,从而可以猜想:任意的a,b∈R+,有
时,分别代入计算,从而可以猜想:任意的a,b∈R+,有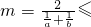
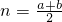 ,当且仅当a=b时取得等号;
,当且仅当a=b时取得等号;(2)类比第(1)小题,对于任意的a,b,c∈R+,猜想:
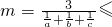
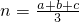 ,当且仅当a=b=c时取得等号利用分析法可以进行证明.
,当且仅当a=b=c时取得等号利用分析法可以进行证明.点评:本题以大小比较为载体,考查基本不等式的运用,考查类比思想,解题的关键是正确运用基本不等式证明不等式.

练习册系列答案
相关题目