题目内容
2. 如图,过四棱柱ABCD-A1B1C1D1形木块上底面内的一点P和下底面的对角线BD将木块锯开,得到截面BDEF.
如图,过四棱柱ABCD-A1B1C1D1形木块上底面内的一点P和下底面的对角线BD将木块锯开,得到截面BDEF.(1)请在木块的上表面作出过P的锯线EF,并说明理由;
(2)若该四棱柱的底面为菱形,四边形BB1D1D是矩形,试证明:平面BDEF⊥平面A1C1CA.
分析 (1)此题实际上是在平面A1B1C1D1形上找到过点P的线段EF,EF∥BD;
(2)欲证明平面BDEF⊥平面A1C1CA,只需证得BD⊥平面A1C1CA.
解答 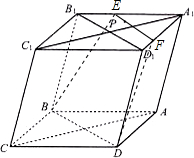 解:(1)在上底面内过点P作B1D1的平行线分别交A1D1、A1B1于F、E两点,则EF即为所作的锯线.
解:(1)在上底面内过点P作B1D1的平行线分别交A1D1、A1B1于F、E两点,则EF即为所作的锯线.
在四棱柱ABCD-A1B1C1D1中,侧棱BB1∥DD1,且BB1=DD1,
所以四边形BB1D1D是平行四边形,B1D1∥BD.
又平面ABCD∥平面A1B1C1D1,平面BDFE∩平面ABCD=BD,平面BDFE∩平面A1B1C1D1=EF,
所以EF∥BD,
从而EF∥B1D1;
(2)证明:由于四边形BB1D1D是矩形,所以BD⊥B1B.
又A1A∥B1B,
∴BD⊥A1A.
又四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,
∴BD⊥AC.
∵AC∩A1A=A,AC?平面A1C1CA,A1A?平面A1C1CA,
∴BD⊥平面A1C1CA.
∵BD?平面BDFE,
∴平面BDFE⊥平面A1C1CA.
点评 本题考查了棱柱的结构特征和平面与平面垂直的判定.解题时利用了“如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直”证得(2)的结论.

练习册系列答案
相关题目
15.第十二届《财富》全球论坛将于2013年6月在成都举行,为了使大会圆满举行,组委会在大学生中招聘了6名志愿者,其中甲大学有2名,乙大学有3名,丙大学有1名,若将他们安排在连续六天的服务工作中,每人一天,那么同一所大学的志愿者不安排在相邻两天服务的概率为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{10}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{6}$ |
12.为了计算1×3×5×7×…×21的结果,设计如图所示的程序框图,则判断框内可填入的条件是( )

| A. | n≤9 | B. | n≤10 | C. | n≤11 | D. | n≤12 |
 如图所示,在三棱锥D-ABC中,AB=BC=CD=1,AC=$\sqrt{3}$,平面ACD⊥平面ABC,∠BCD=90°
如图所示,在三棱锥D-ABC中,AB=BC=CD=1,AC=$\sqrt{3}$,平面ACD⊥平面ABC,∠BCD=90°
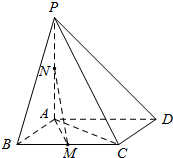 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M,N分别为BC,PA的中点,且AB=AC=1,AD=$\sqrt{2}$.