Question

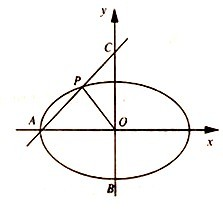在直角坐标平面xOy中，椭圆E：

x2

4

+y²=1的左顶点为A，下顶点为B．
（1）求圆心在y轴上且过两点A，B的圆方程；
（2）过点A作直线l交椭圆于点P，交y正半轴于点C，若△OAP与△OCP的面积相等，求直线l的斜率k．

Answer 1

分析：（1）椭圆E：

x2

4

+y²=1的a=2，b=1，c=

3

，得出左顶点和下顶点，线段AB的垂直平分线与y轴的交点即圆心在y轴上且过两点A，B的圆的圆心坐标为（0，0），从而得出圆的半径，最后写出圆心在y轴上且过两点A，B的圆方程．
（2）根据△OAP与△OCP的面积相等，得到P是线段AC的中点，设C（0，2n），则P（1，n）代入椭圆的方程得C的坐标，利用斜率得出直线l的斜率即可．

解答：解：（1）∵椭圆E：

x2

4

+y²=1的
a=2，b=1，c=

3

，
∴左顶点为A（-2，0），下顶点为B（0，-1）．
线段AB的垂直平分线的方程为：y-（-

1

2

）=2（x+1）
令x=0得它与y轴的交点坐标为（0，

3

2

），
即圆心在y轴上且过两点A，B的圆的圆心坐标为（0，

3

2

），
故其半径r=1+

3

2

=

5

2

，
∴圆心在y轴上且过两点A，B的圆方程：x²+（y-

3

2

）²=

25

4

；
（2）∵△OAP与△OCP的面积相等，
∴P是线段AC的中点，
设C（0，2n），则P（-1，n）代入椭圆的方程得：

1

4

+n 2=1，又点A作直线l交椭圆于点P，交y正半轴于点C，故n=

3

2

，
∴C（0，

3

），又A（-2，0），
直线l的斜率k=

3 -0

0-(-2)

=

3

2

．

点评：本小题主要考查圆的标准方程、椭圆的简单性质、直线的斜率等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．