题目内容
已知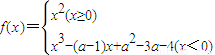 在(-∞,+∞)上是增函数,则实数a的取值范围是( )
在(-∞,+∞)上是增函数,则实数a的取值范围是( )A.(-∞,1]
B.[-1,4]
C.[-1,1]
D.(-∞,1)
【答案】分析:要是一个分段函数在实数上是一个增函数,需要两段都是增函数且两个函数的交点处要满足递增,当x小于0时,要使的函数是一个减函数,求导以后导函数横小于0,注意两个端点处的大小关系.
解答:解:∵要是一个分段函数在实数上是一个增函数.
需要两段都是增函数且两个函数的交点处要满足递增,
当x<0时,y′=3x2-(a-1)>0恒成立,
∴a-1<3x2
∴a-1≤0
∴a≤1,
当x=0时,a2-3a-4≤0
∴-1≤a≤4,
综上可知-1≤a≤1
故选C.
点评:本题考查函数的单调性,分段函数的单调性,解题的关键是在两个函数的分界处,两个函数的大小关系一定要写清楚.
解答:解:∵要是一个分段函数在实数上是一个增函数.
需要两段都是增函数且两个函数的交点处要满足递增,
当x<0时,y′=3x2-(a-1)>0恒成立,
∴a-1<3x2
∴a-1≤0
∴a≤1,
当x=0时,a2-3a-4≤0
∴-1≤a≤4,
综上可知-1≤a≤1
故选C.
点评:本题考查函数的单调性,分段函数的单调性,解题的关键是在两个函数的分界处,两个函数的大小关系一定要写清楚.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
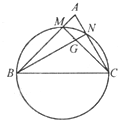 (2013•成都一模)如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若
(2013•成都一模)如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若