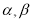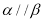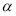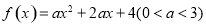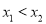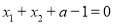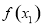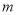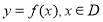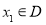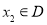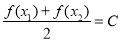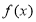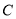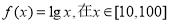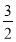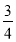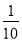题目内容
已知函数 .
.
(1)若 在
在 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;
(2)当 时,若对任意的
时,若对任意的 ,总存在
,总存在 使
使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)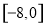 ;(2)
;(2)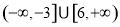 .
.
【解析】
试题分析:(1)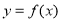 在
在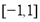 上存在零点,只需
上存在零点,只需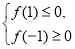 即可;
即可;
(2)本问是存在性问题,只需函数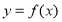 的值域为函数
的值域为函数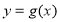 的值域的子集即可.
的值域的子集即可.
试题解析:(1)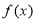 的对称轴为
的对称轴为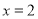 ,所以
,所以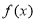 在
在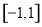 上单调递减,且函数
上单调递减,且函数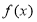 在
在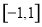 存在零点,所以
存在零点,所以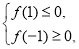 即
即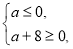 解得
解得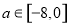 .
.
故实数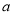 的取值范围为
的取值范围为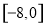 .
.
(2)由题可知函数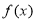 的值域为函数
的值域为函数 的值域的子集
的值域的子集
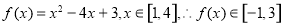 ,
,
以下求函数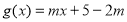 的值域:
的值域:
①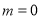 时,
时,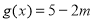 为常函数,不符合题意;
为常函数,不符合题意;
②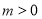 ,
,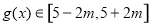 ,∴
,∴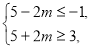 解得
解得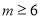 ;
;
③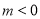 ,
,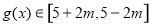 ,∴
,∴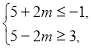 解得
解得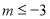 .
.
综上所述,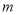 的取值范围为
的取值范围为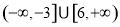 .
.
考点:1.函数的零点;2.恒成立问题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目