题目内容
在直角坐标系中,点A在圆x2+y2=2y上,点B在直线y=x-1上.则|AB|最小值为( )
分析:根据点到直线的距离公式求出圆心到直线的距离,判断出直线和圆的位置关系;再求出圆心到直线的最小值,即可求线段AB有最小值
解答:解:∵圆心(0,1)到直线x-y+1=0的距离d=
=
>1
∴圆和直线相离.
圆心到直线的最短距离为
.
故线段AB的最小值为:d-r=
-1.
故选A
| |1-0+1| | ||
|
| 2 |
∴圆和直线相离.
圆心到直线的最短距离为
| 2 |
故线段AB的最小值为:d-r=
| 2 |
故选A
点评:本题主要考查点到直线的距离公式的应用以及圆和直线的位置关系判断.属于基础试题

练习册系列答案
相关题目
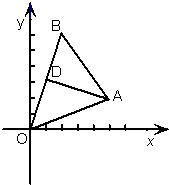 如图在直角坐标系中,点A(5,2),B(2,m)AD⊥OB,垂足为D,
如图在直角坐标系中,点A(5,2),B(2,m)AD⊥OB,垂足为D,



