题目内容
定义在R上的函数y=f(x)是增函数,且函数y=f(x-3)的图象关于(3,0)成中心对称,若s,t满足不等式f(s2-2s)≥-f(2t-t2),当1≤s≤4时,则t2+s2-2s的取值范围为( )
分析:由已知中定义在R上的函数y=f(x)是增函数,且函数y=f(x-3)的图象关于(3,0)成中心对称,易得函数y=f(x)是奇函数,根据函数单调性和奇偶性的性质可得s2-2s≥t2-2t,进而得到s与t的关系式,最后找到目标函数z=t2+s2-2s=t2+(s-1)2-1,利用线性规划问题进行解决.
解答:解:y=f(x-3)的图象相当于y=f(x)函数图象向右移了3个单位.
又由于y=f(x-3)图象关于(3,0)点对称,
向左移回3个单位即表示y=f(x)函数图象关于(0,0)点对称,故函数是奇函数.
所以f(2t-t2)=-f(t2-2t),即f(s2-2s)≥f(t2-2t).
因为y=f(x)函数是增函数,所以s2-2s≥t2-2t,移项得:s2-2s-t2+2t≥0,
即:(s-t)(s+t-2)≥0,解得:s≥t且s+t≥2,或s≤t且s+t≤2.
转化为线性规划问题:已知s≥t且s+t≥2,且1≤s≤4,目标函数:z=t2+s2-2s=t2+(s-1)2-1,
画出可行域:
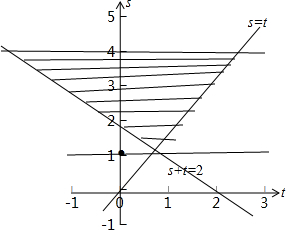
z=t2+s2-2s 的最值,转化为可行域中的点到点(0,1)距离的平方减去1,
z=t2+s2-2s=t2+(s-1)2-1,
∴z的最小值为点(0,1)到直线s+t=2距离的平方减去1,∴zmin=(
)2-1=-
,
z的最大值为点(0,1)到点(4,4)距离的平方减去1,
zmax=(-4)2+(-3)2-1=24,∴-
≤z≤24.
当s≤t且s+t≤2,且1≤s≤4,可行域不存在,舍去;
∴t2+s2-2s 的取值范围是[-
,24],
故选 D.
又由于y=f(x-3)图象关于(3,0)点对称,
向左移回3个单位即表示y=f(x)函数图象关于(0,0)点对称,故函数是奇函数.
所以f(2t-t2)=-f(t2-2t),即f(s2-2s)≥f(t2-2t).
因为y=f(x)函数是增函数,所以s2-2s≥t2-2t,移项得:s2-2s-t2+2t≥0,
即:(s-t)(s+t-2)≥0,解得:s≥t且s+t≥2,或s≤t且s+t≤2.
转化为线性规划问题:已知s≥t且s+t≥2,且1≤s≤4,目标函数:z=t2+s2-2s=t2+(s-1)2-1,
画出可行域:

z=t2+s2-2s 的最值,转化为可行域中的点到点(0,1)距离的平方减去1,
z=t2+s2-2s=t2+(s-1)2-1,
∴z的最小值为点(0,1)到直线s+t=2距离的平方减去1,∴zmin=(
| |-1| |
| 2 |
| 1 |
| 2 |
z的最大值为点(0,1)到点(4,4)距离的平方减去1,
zmax=(-4)2+(-3)2-1=24,∴-
| 1 |
| 2 |
当s≤t且s+t≤2,且1≤s≤4,可行域不存在,舍去;
∴t2+s2-2s 的取值范围是[-
| 1 |
| 2 |
故选 D.
点评:本题考查的知识点是抽象函数及其应用,函数单调性的性质,其中根据已知条件得到函数为奇函数,进而将不等式f(s2-2s)≥-f(2t-t2),转化为s2-2s≥t2-2t,最后转化到线性规划问题上解决,就比较简单了,属于中档题.

练习册系列答案
相关题目