题目内容
函数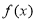
，
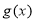的定义域都是
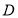，直线
（
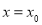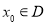），与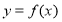
，
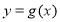的图象分别交于
，
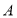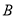两点，若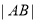
的值是不等于
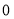的常数，则称曲线
，
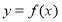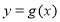为“平行曲线”，设
（
，
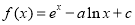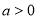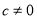），且
，
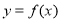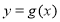为区间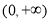
的“平行曲线”，
，
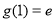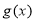在区间
上的零点唯一，则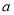
的取值范围是 ．
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
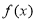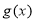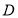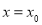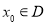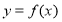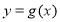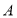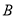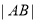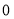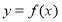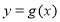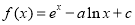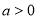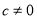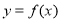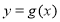函数，的定义域都是，直线（），与，的图象分别交于，两点，若的值是不等于的常数，则称曲线，为“平行曲线”，设（，），且，为区间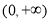的“平行曲线”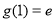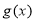，，在区间上的零点唯一，则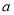的取值范围是 ．
阅读快车系列答案
中，角
所对的边分别为
，且
．
的值；
，求
的值．
中，曲线
的参数方程为
（
为参数），以原点
为极点，
轴正半轴为极轴（两坐标系取区间的长度单位）的极坐标系中，曲线
：
．
的普通方程与曲线
的直角坐标方程；
，
分别是曲线
和曲线
上的动点，求
最小值． 
在
处取到极值，则
的值为（ ）
B．
C．
D．
，函数
．
，求曲线
在
处的切线方程；
无零点，求实数
的取值范围；
有两个相异零点
，
，求证：
．
B．
C．
D．
的图象关于
轴对称，且对任意
都有
，若当
时，
，则
（ ）
B．
C.
D．4
，且被交点平分，另一条弦被交点分成1:4两部分，则这条弦长是（ ）
B．
D．